Advertisements
Advertisements
प्रश्न
Find the remainder when x3 + 3x2 + 3x + 1 is divided by x+1.
उत्तर १
Let p(x) = x3 + 3x2 + 3x + 1
x+1 = 0 ⇒ x = -1
∴ Remainder = p(-1) = (-1)3 + 3(-1)2 + 3(-1) + 1
= -1 + 3 - 3 + 1
= 0
Therefore, the remainder is 0.
उत्तर २
By long division,
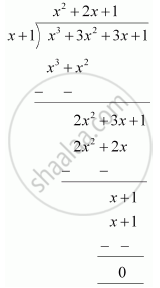
Therefore, the remainder is 0.
APPEARS IN
संबंधित प्रश्न
Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 – kx + 5 by x – 2, leaves a remainder 7.
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Using the Remainder Theorem, factorise the following completely:
2x3 + x2 – 13x + 6
Using the Remainder Theorem, factorise the following completely:
4x3 + 7x2 – 36x – 63
Using the Remainder Theorem, factorise the following completely:
x3 + x2 – 4x – 4
Find the value of ‘m’, if mx3 + 2x2 – 3 and x2 – mx + 4 leave the same remainder when each is divided by x – 2.
Using remainder theorem, find the remainder on dividing f(x) by (x + 3) where f(x) = 3x3 + 7x2 – 5x + 1
Use the Remainder Theorem to factorise the following expression:
2x3 + x2 – 13x + 6
When 2x3 – x2 – 3x + 5 is divided by 2x + 1, then the remainder is
By Remainder Theorem find the remainder, when p(x) is divided by g(x), where p(x) = 4x3 – 12x2 + 14x – 3, g(x) = 2x – 1
