Advertisements
Advertisements
प्रश्न
Find the roots of the following quadratic equations, if they exist, by the method of completing the square `4x^2 + 4sqrt3x + 3 = 0`
उत्तर
`4x^2 + 4sqrt3x + 3 = 0`
`⇒ (2x)^2 + 2 × 2x × sqrt3 + (sqrt3)^2 = 0`
`⇒ (2x + sqrt3)^2 = 0`
`⇒ (2x + sqrt3) = 0 `
`⇒ x = (-sqrt3)/2 `
APPEARS IN
संबंधित प्रश्न
Find the roots of the following quadratic equations (if they exist) by the method of completing the square.
`sqrt3x^2+10x+7sqrt3=0`
The sum of the areas of two squares is `640m^2` . If the difference in their perimeter be 64m, find the sides of the two square
The area of right -angled triangle is 165 sq meters. Determine its base and altitude if the latter exceeds the former by 7 meters.
The hypotenuse of a right-angled triangle is 1 meter less than twice the shortest side. If the third side 1 meter more than the shortest side, find the side, find the sides of the triangle.
Fill in the gaps and complete.
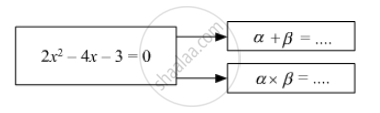
If α, β are roots of quadratic equation,
Determine the nature of roots of the following quadratic equation.
x2 – 4x + 4 = 0
Sum of the roots of a quadratic equation is double their product. Find k if equation x2 – 4kx + k + 3 = 0
α, β are roots of y2 – 2y –7 = 0 find,
α3 + β3
If p2x2 – q2 = 0, then x =?
If a, b, care in continued proportion, then show that `(a + b)^2/(ab) = (b + c)^2/(bc)`.
Since a, b, c are in continued proportion
∴ `a/b = square/square` = k(say)
⇒ b = `square`, a = `square` = `square`.k = `square`.k2
Now, L.H.S. = `(a + b)^2/(a.square) = (square + square)^2/(square*square)`
= `(squarek^2(k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
R.H.S. = `(b + c)^2/(b.square) = (square + square)^2/(square*square) = (square (k + 1)^2)/(square*square)`
= `(k + 1)^2/square`
L.H.S. = `square`
