Advertisements
Advertisements
प्रश्न
Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
उत्तर
Let us assume that the required displacement is x.
∴ The potential energy of the simple harmonic oscillator = `1/2 kx^2`
Where, k = force constant = `mω^2`
∴ P.E. = `1/2 mω^2x^2` ......(i)
The maximum energy of the oscillator
TE = `1/2 mω^2A^2` [∵ xmax = A] ......(ii)
Where, A = Amplitude of motion
Given, P.E. = `1/2` TE
⇒ `1/2 mω^2x^2 = 1/2 [1/2 mω^2A^2]`
⇒ `x^2 = A^2/2`
or `x = sqrt(A^2/2) = +- A/sqrt(2)`
Sign ± indicates either side of mean position.
APPEARS IN
संबंधित प्रश्न
The maximum speed and acceleration of a particle executing simple harmonic motion are 10 cm/s and 50 cm/s2. Find the position(s) of the particle when the speed is 8 cm/s.
A particle having mass 10 g oscillates according to the equation x = (2.0 cm) sin [(100 s−1)t + π/6]. Find (a) the amplitude, the time period and the spring constant. (c) the position, the velocity and the acceleration at t = 0.
A block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314 s. Find the maximum force exerted by the spring on the block.
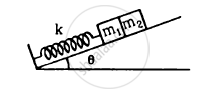
The block of mass m1 shown in figure is fastened to the spring and the block of mass m2 is placed against it. (a) Find the compression of the spring in the equilibrium position. (b) The blocks are pushed a further distance (2/k) (m1 + m2)g sin θ against the spring and released. Find the position where the two blocks separate. (c) What is the common speed of blocks at the time of separation?
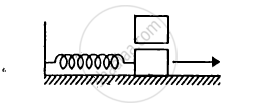
A 1 kg block is executing simple harmonic motion of amplitude 0.1 m on a smooth horizontal surface under the restoring force of a spring of spring constant 100 N/m. A block of mass 3 kg is gently placed on it at the instant it passes through the mean position. Assuming that the two blocks move together, find the frequency and the amplitude of the motion.
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
An object of mass 0.5 kg is executing a simple Harmonic motion. Its amplitude is 5 cm and the time period (T) is 0.2 s. What will be the potential energy of the object at an instant t = `T/4` s starting from the mean position? Assume that the initial phase of the oscillation is zero.
A particle undergoing simple harmonic motion has time dependent displacement given by x(t) = A sin`(pit)/90`. The ratio of kinetic to the potential energy of this particle at t = 210s will be ______.
