Advertisements
Advertisements
प्रश्न
Find the equation of circles that touch both the axes and pass through (− 4, −2) in general form
उत्तर
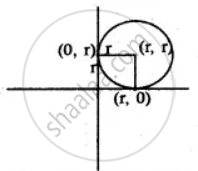
Since the circle touches both the axes
Its centre will be (r, r) and the radius will be r.
Here centre = C = (r, r) and point on the circle is A = (− 4, −2)
CA = r
⇒ CA2 = r2
(i.e) (r + 4)2 + (r + 2)2 = r2
⇒ r2 + 8r +16 + r2 + 4r + 4 – r2 = 0
(i.e) r2 + 12r + 20 = 0
(r + 2)(r + 10) = 0
⇒ r = − 2 or − 10
When r = − 2, the equation of the circle will be (x + 2)2 + (y + 2)2 = 22
(i.e) x2 + y2 + 4x + 4y + 4 = 0
When r = −10, the equation of the circle will be (x + 10)2 + (y + 10)2 = 102
(i.e) x2 + y2 + 20x + 20y + 100 = 0
APPEARS IN
संबंधित प्रश्न
Find the equation of the following circles having the centre (3, 5) and radius 5 units.
Find the equation of the following circles having the centre (0,0) and radius 2 units
Find the equation of the circle whose centre is (2, 3) and which passes through (1, 4).
Find the length of the tangent from (1, 2) to the circle x2 + y2 – 2x + 4y + 9 = 0.
(1, -2) is the centre of the circle x2 + y2 + ax + by – 4 = 0, then its radius:
The centre of the circle x2 + y2 – 2x + 2y – 9 = 0 is:
If the perimeter of the circle is 8π units and centre is (2, 2) then the equation of the circle is:
The equation of the circle with centre (3, -4) and touches the x-axis is:
If the circle touches the x-axis, y-axis, and the line x = 6 then the length of the diameter of the circle is:
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 = 0 and 4x + y – 27 = 0
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
Find centre and radius of the following circles
x2 + (y + 2)2 = 0
Find centre and radius of the following circles
x2 + y2 + 6x – 4y + 4 = 0
Find centre and radius of the following circles
2x2 + 2y2 – 6x + 4y + 2 = 0
Choose the correct alternative:
The circle x2 + y2 = 4x + 8y + 5 intersects the line 3x – 4y = m at two distinct points if
Choose the correct alternative:
The length of the diameter of the circle which touches the x -axis at the point (1, 0) and passes through the point (2, 3)
Choose the correct alternative:
The radius of the circle passing through the points (6, 2) two of whose diameter are x + y = 6 and x + 2y = 4 is
