Advertisements
Advertisements
Question
Find the equation of circles that touch both the axes and pass through (− 4, −2) in general form
Solution
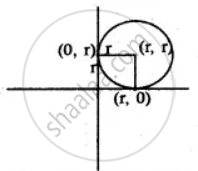
Since the circle touches both the axes
Its centre will be (r, r) and the radius will be r.
Here centre = C = (r, r) and point on the circle is A = (− 4, −2)
CA = r
⇒ CA2 = r2
(i.e) (r + 4)2 + (r + 2)2 = r2
⇒ r2 + 8r +16 + r2 + 4r + 4 – r2 = 0
(i.e) r2 + 12r + 20 = 0
(r + 2)(r + 10) = 0
⇒ r = − 2 or − 10
When r = − 2, the equation of the circle will be (x + 2)2 + (y + 2)2 = 22
(i.e) x2 + y2 + 4x + 4y + 4 = 0
When r = −10, the equation of the circle will be (x + 10)2 + (y + 10)2 = 102
(i.e) x2 + y2 + 20x + 20y + 100 = 0
APPEARS IN
RELATED QUESTIONS
Find the centre and radius of the circle
x2 + y2 = 16
Find the centre and radius of the circle.
(x + 2) (x – 5) + (y – 2) (y – 1) = 0
Find the equation of the circle passing through the points (0, 1), (4, 3) and (1, -1).
If the lines x + y = 6 and x + 2y = 4 are diameters of the circle, and the circle passes through the point (2, 6) then find its equation.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Find the equation of the tangent to the circle x2 + y2 – 4x + 4y – 8 = 0 at (-2, -2).
Find the values of a and b if the equation (a - 1)x2 + by2 + (b - 8)xy + 4x + 4y - 1 = 0 represents a circle.
The length of the tangent from (4, 5) to the circle x2 + y2 = 16 is:
In the equation of the circle x2 + y2 = 16 then v intercept is (are):
If the perimeter of the circle is 8π units and centre is (2, 2) then the equation of the circle is:
Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form
Find the equation of the circle with centre (2, −1) and passing through the point (3, 6) in standard form
Obtain the equation of the circle for which (3, 4) and (2, -7) are the ends of a diameter.
A circle of area 9π square units has two of its diameters along the lines x + y = 5 and x – y = 1. Find the equation of the circle
If y = `2sqrt(2)x + "c"` is a tangent to the circle x2 + y2 = 16, find the value of c
Find centre and radius of the following circles
x2 + y2 + 6x – 4y + 4 = 0
Find centre and radius of the following circles
x2 + y2 – x + 2y – 3 = 0
If the equation 3x2 + (3 – p)xy + qy2 – 2px = 8pq represents a circle, find p and q. Also determine the centre and radius of the circle
Choose the correct alternative:
If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)2 + (y + 2)2 = r2, then the value of r2 is
