Advertisements
Advertisements
Question
Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form
Solution
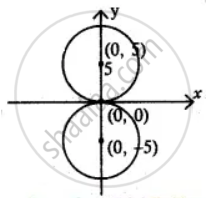
Given radius = 5 cm and the circle is touching x-axis
So centre will be (0, ± 5) and radius = 5
The equation of the circle with centre (0, ± 5) and radius 5 units is
(x – 0)2 + (y ± 5)2 = 52
(i.e) x2 + y2 ± 10 y + 25 – 25 = 0
(i.e) x2 + y2 ± 10y = 0
APPEARS IN
RELATED QUESTIONS
Find the centre and radius of the circle.
5x2 + 5y2+ 4x – 8y – 16 = 0
Find the centre and radius of the circle.
(x + 2) (x – 5) + (y – 2) (y – 1) = 0
If the lines x + y = 6 and x + 2y = 4 are diameters of the circle, and the circle passes through the point (2, 6) then find its equation.
Find the equation of the circle having (4, 7) and (-2, 5) as the extremities of a diameter.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Find the value of P if the line 3x + 4y – P = 0 is a tangent to the circle x2 + y2 = 16.
(1, -2) is the centre of the circle x2 + y2 + ax + by – 4 = 0, then its radius:
The centre of the circle x2 + y2 – 2x + 2y – 9 = 0 is:
The equation of the circle with centre on the x axis and passing through the origin is:
Find the equation of circles that touch both the axes and pass through (− 4, −2) in general form
Find the equation of the circle through the points (1, 0), (– 1, 0) and (0, 1)
Determine whether the points (– 2, 1), (0, 0) and (– 4, – 3) lie outside, on or inside the circle x2 + y2 – 5x + 2y – 5 = 0
Find centre and radius of the following circles
x2 + (y + 2)2 = 0
Choose the correct alternative:
The equation of the circle passing through (1, 5) and (4, 1) and touching y-axis `x^2 + y^2 - 5x - 6y + 9 + lambda(4x + 3y - 19)` = where `lambda` is equal to
Choose the correct alternative:
The radius of the circle 3x2 + by2 + 4bx – 6by + b2 = 0 is
Choose the correct alternative:
The equation of the normal to the circle x2 + y2 – 2x – 2y + 1 = 0 which is parallel to the line 2x + 4y = 3 is
Choose the correct alternative:
The radius of the circle passing through the points (6, 2) two of whose diameter are x + y = 6 and x + 2y = 4 is
