Advertisements
Advertisements
प्रश्न
Find the sum of the following APs.
0.6, 1.7, 2.8, …….., to 100 terms.
उत्तर
0.6, 1.7, 2.8, …, to 100 terms
For this A.P.,
a = 0.6
d = a2 − a1
= 1.7 − 0.6
d = 1.1
n = 100
We know that
Sn = `n/2[2a+(n-1)d]`
S100 = `100/2[2(0.6)+(100 - 1)1.1]`
= 50[1.2 + (99) × (1.1)]
= 50[1.2 + 108.9]
= 50[110.1]
= 5505
Thus, the required sum of first 100 terms is 5505.
संबंधित प्रश्न
Find the sum of all numbers from 50 to 350 which are divisible by 6. Hence find the 15th term of that A.P.
In an A.P., if S5 + S7 = 167 and S10=235, then find the A.P., where Sn denotes the sum of its first n terms.
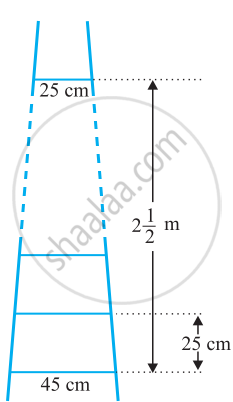
A ladder has rungs 25 cm apart. (See figure). The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. If the top and bottom rungs are 2 `1/2` m apart, what is the length of the wood required for the rungs?
[Hint: number of rungs = `250/25+ 1`]
If the nth term of the A.P. 9, 7, 5, ... is same as the nth term of the A.P. 15, 12, 9, ... find n.
Find the sum 3 + 11 + 19 + ... + 803
The 4th term of an AP is 11. The sum of the 5th and 7th terms of this AP is 34. Find its common difference
How many two-digits numbers are divisible by 3?
Find the first term and common difference for the A.P.
5, 1, –3, –7,...
The A.P. in which 4th term is –15 and 9th term is –30. Find the sum of the first 10 numbers.
If the first, second and last term of an A.P. are a, b and 2a respectively, its sum is
If the first term of an A.P. is 2 and common difference is 4, then the sum of its 40 terms is
If 18th and 11th term of an A.P. are in the ratio 3 : 2, then its 21st and 5th terms are in the ratio
Suppose three parts of 207 are (a − d), a , (a + d) such that , (a + d) >a > (a − d).
Suppose the angles of a triangle are (a − d), a , (a + d) such that , (a + d) >a > (a − d).
Find the sum of first 20 terms of an A.P. whose first term is 3 and the last term is 57.
Find the sum of all the 11 terms of an AP whose middle most term is 30.
Yasmeen saves Rs 32 during the first month, Rs 36 in the second month and Rs 40 in the third month. If she continues to save in this manner, in how many months will she save Rs 2000?
Jaspal Singh repays his total loan of Rs. 118000 by paying every month starting with the first instalment of Rs. 1000. If he increases the instalment by Rs. 100 every month, what amount will be paid by him in the 30th instalment? What amount of loan does he still have to pay after the 30th instalment?
The nth term of an A.P. is 6n + 4. The sum of its first 2 terms is ______.
