Advertisements
Advertisements
प्रश्न
Find the total surface area of frustum, if its radii are 15 cm and 7 cm. Also, the slant height of the frustum is 14 cm.
Radii of the frustum = `square` cm and `square` cm
Slant height of the frustum = `square` cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7 [square + square + (square + square) square]`
= `22/7 (square)`
= `square` cm2
Hence, the total surface area of the frustum is `square`.
उत्तर
Radii of the frustum = 15 cm and 7 cm
Slant height of the frustum = 14 cm
Total surface area = `π[(r_1^2 + r_2^2 + (r_1 + r_2)l]`
= `22/7` [(15)2 + (7)2 + (15 + 7) 14]
= `22/7 (bb582)`
= 1829.14 cm2
Hence, the total surface area of the frustum is 1829.14 cm2.
APPEARS IN
संबंधित प्रश्न
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass. [use π=22/7]
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. find the curved surface area of the frustum.
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
A solid toy s in the form of a hemisphere surrounded by a right circular cone . The height of cone is 4 cm and the diameter of the base is 8 cm . Determine the volume of the toy. If a cube circumscribes the toy , then find the difference of the volumes of cube and the toy .
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown in fig. 16.77. Calculate the volume of icecream , provided that its 1/ 6 part is left unfilled with icecream .
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces?
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the ratio of the volumes of the upper part and the cone is
A solid metal cone with base radius of 12 cm and height 24 cm is melted to form solid spherical balls of diameter 6 cm each. Find the number of balls thus formed.
A spherical cannon ball, 28 cm in diameter, is melted and recast into a right circular conical mould with base diameter of 35 cm. Find the height of the cone.
A hemisphere of lead of radius 9 cm is cast into a right circular cone of height 72 cm. Find the radius of the base of the cone.
A container, open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm, respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre.
A bucket is in the form of a frustum of a cone and it can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, then find the height of the bucket.
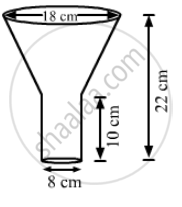
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, then find the area of the tin sheet required to make the funnel.
The circular ends of a bucket are of radii 35 cm and 14 cm and the height of the bucket is 40 cm. Its volume is
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.
The slant height of a frustum of a cone is 4 m and the perimeter of circular ends is 18 m and 16 m. Find the cost of painting its curved surface area at ₹ 100 per sq. m
A shuttle cock used for playing badminton has the shape of the combination of ______.
