Advertisements
Advertisements
प्रश्न
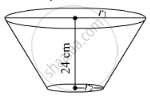
The circular ends of a bucket are of radii 35 cm and 14 cm and the height of the bucket is 40 cm. Its volume is
पर्याय
60060 cm3
80080 cm3
70040 cm3
80160 cm3
उत्तर
80080 cm3
Let R and r be the radii of the top and base of the bucket, respectively, and let h be its height.
Then,
R = 35 cm, r = 14 cm , h = 40 cm
R = 35 cm, r = 14 cm, h = 40 cm
Volume of the bucket = Volume of the frustum of the cone
`=1/3pi"h"["R"^2 +"r"^2+"Rr" ] "cm"^3`
`= 1/3 xx22/7xx40xx[(35)^2 + (14)^2 + (35xx14)] "cm"^3`
`=((880)/(21)xx1911) "cm"^3`
= 80080 cm3
Hence, the volume of the bucket is 80080 cm3.
APPEARS IN
संबंधित प्रश्न
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see the figure given below). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material use for making it. [use π=22/7]

The radii of the ends of a frustum are 14 cm and 6 cm respectively and its height is 6 cm. Find its curved surface area.
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base . Compare the volumes of two parts.
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the values of \[\frac{H}{R} .\]
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. The height of the cone is
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

A drinking glass is in the shape of the frustum of a cone of height 21 cm with 6 cm and 4 cm as the diameters of its two circular ends. Find the capacity of the glass.
An open metal bucket is in the shape of a frustum of a cone, mounted on a hollow cylindrical base made of the same metallic sheet. The diameters of the two circular ends of the bucket are 45 cm and 25 cm, the total vertical height of the bucket is 40 cm and that of the cylindrical base is 6 cm. Find the area of the metallic sheet used to make the bucket. Also, find the volume of water the bucket can hold, in litres.
