Advertisements
Advertisements
प्रश्न
Find the value, of k, if the line represented by kx – 5y + 4 = 0 and 4x – 2y + 5 = 0 are perpendicular to each other.
उत्तर
Here, kx - 5y + 4 = 0
⇒ y = `(kx)/(5) + (4)/(5)`
∴ The slope of the line is `k/(5)`.
Also 4x - 2y + 5 = 0
y = `2x + (5)/(2)`
∴ The slope of line is 2.
Since, the given lines are perpendicular to each other, we have
`(k/5)(2)` = -1
⇒ k = `(-5)/(2)`.
APPEARS IN
संबंधित प्रश्न
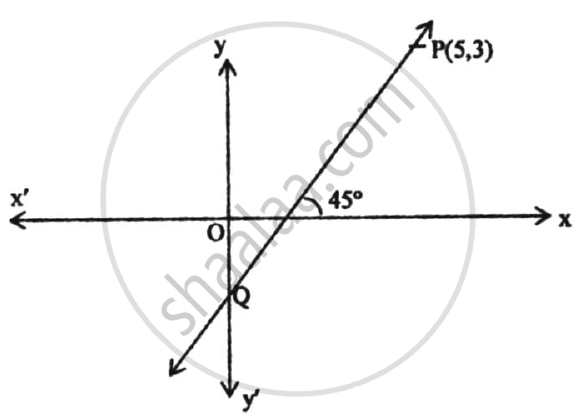
The line through P(5, 3) intersects y-axis at Q.
(1) Write the slope of the line.
(2) Write the equation of the line.
(3) Find the coordinates of Q.
Find the slope of the line parallel to AB if : A = (0, −3) and B = (−2, 5)
The slope of the side BC of a rectangle ABCD is `2/3`. Find:
- the slope of the side AB.
- the slope of the side AD.
Find the slope of the line which is perpendicular to `x - y/2 + 3 = 0`
Angles made by the line with the positive direction of X–axis is given. Find the slope of these line.
60°
Determine whether the following point is collinear.
P(2, –5), Q(1, –3), R(–2, 3)
Find the type of the quadrilateral if points A(–4, –2), B(–3, –7) C(3, –2) and D(2, 3) are joined serially.
Find the slope of a line parallel to the given line 5x + 2y = 11
Find the image of a point (-1, 2) in the line joining (2, 1) and (- 3, 2).
If the lines 7y = ax + 4 and 2y = 3 − x, are parallel to each other, then the value of ‘a’ is:
