गणित के एक टेस्ट में, 33 विद्यार्थियों द्वारा (100 में से) प्राप्त किए गए अंक निम्नलिखित हैं : 69, 48, 84, 58, 48, 73, 83, 48, 66, 58, 84, 66, 64, 71, 64, 66, 69, 66, 83, 66, 69, 71 - Mathematics (गणित)

गणित के एक टेस्ट में, 33 विद्यार्थियों द्वारा (100 में से) प्राप्त किए गए अंक निम्नलिखित हैं :

69, 48, 84, 58, 48, 73, 83, 48, 66, 58, 84, 66, 64, 71, 64, 66, 69, 66, 83, 66, 69, 71, 81, 71, 73, 69, 66, 66, 64, 58, 64, 69, 69

इन आँकड़ों को एक बारंबारता बंटन द्वारा निरूपित कीजिए।

बेरीज

गणित में समान अंक प्राप्त करने वाले विद्यार्थियों की संख्या को उस अंक की बारंबारता कहते हैं।

दिए गए आँकड़ों के लिए एक बारंबारता वितरण तालिका नीचे दी गई है -

shaalaa.com

केन्द्रीय प्रवृत्ति के माप

या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?

पाठ 14: सांख्यिकी और प्रायिकता - प्रश्नावली 14.3 [पृष्ठ १४३]

पाठ 14 सांख्यिकी और प्रायिकता
प्रश्नावली 14.3 | Q 3. | पृष्ठ १४३

एक टीम ने फुटबाल के 10 मैचों में निम्नलिखित गोल किए : 2, 3,4, 5, 0, 1, 3, 3, 4, 3 इन गोलों के माध्य, माध्यक और बहुलक ज्ञात कीजिए।

पाँच संख्याओं का माध्य 30 है। यदि इनमें से एक संख्या को हटा दिया जाए, तो उनका माध्य 28 हो जाता है। हटाई गई संख्या है

यदि x₁, x₂, ..., x_n का माध्य `barx` है, तो a ≠ 0, के लिए `ax_1, ax_2, ..., ax_n, x_1/a, x_2/a, ..., x_n/a` का माध्य है

78, 56, 22, 34, 45, 54, 39, 68, 54, 84 आँकड़ों का माध्यक है

4, 4, 5, 7, 6, 7, 7, 12, 3 संख्याओं का माध्यक है :

दो सिक्कों को 1000 बार उछाला जाता है और इनके परिणाम निम्नलिखित प्रकार से रिकार्ड किए जाते हैं :

चितों की संख्या	2	1	0
बारंबारता	200	550	250

इस सूचना के आधार पर अधिकतम एक चित की प्रायिकता है :

निम्नलिखित आँकड़ों से एक सतत बारंबारता बंटन तैयार कीजिए :

वर्ग अंतरालों के माप भी ज्ञात कीजिए।

निम्नलिखित बंटन का माध्य ज्ञात कीजिए :

दस प्रेक्षणों 6, 14, 15, 17, x + 1, 2x – 13, 30, 32, 34 और 43 को आरोही क्रम में लिखा गया है। इन आँकड़ों का माध्यक 24 है। x का मान ज्ञात कीजिए।

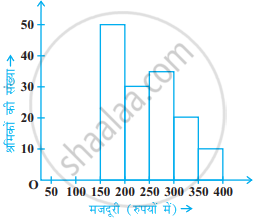
निम्नलिखित आकृति में, एक आयतचित्र दिया है जो किसी फैक्ट्री की श्रमिकों की दैनिक मजदूरी दर्शाता है। इसके लिए एक बारंबारता बंटन सारणी की रचना कीजिए।