Advertisements
Advertisements
प्रश्न
Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?
उत्तर
Each signal requires the use of 2 flags.
There will be as many flags as there are ways of filling in 2 vacant places  in succession by the given 5 flags of different colours.
in succession by the given 5 flags of different colours.
The upper vacant place can be filled in 5 different ways by any one of the 5 flags, following which, the lower vacant place can be filled in 4 different ways by any one of the remaining 4 different flags.
Thus, by multiplication principle, the number of different signals that can be generated is 5 × 4 = 20
APPEARS IN
संबंधित प्रश्न
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is not allowed?
How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is allowed?
How many two-letter words can be formed using letters from the word SPACE, when repetition of letters is not allowed?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is allowed?
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits are not allowed?
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated?
Select the correct answer from the given alternatives.
A college offers 5 courses in the morning and 3 in the evening. The number of ways a student can select exactly one course, either in the morning or in the evening
Answer the following:
A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.
A person went to a restaurant for dinner. In the menu card, the person saw 10 Indian and 7 Chinese food items. In how many ways the person can select either an Indian or a Chinese food?
How many two-digit numbers can be formed using 1, 2, 3, 4, 5 without repetition of digits?
A mobile phone has a passcode of 6 distinct digits. What is the maximum number of attempts one makes to retrieve the passcode?
Given four flags of different colours, how many different signals can be generated if each signal requires the use of three flags, one below the other?
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8 if repetitions of digits is not allowed
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if the repetition of digits is not allowed
Count the numbers between 999 and 10000 subject to the condition that there are no digit is repeated
To travel from a place A to place B, there are two different bus routes B1, B2, two different train routes T1, T2 and one air route A1. From place B to place C there is one bus route say B1, two different train routes say T1, T2 and one air route A1. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation
How many strings can be formed using the letters of the word LOTUS if the word either starts with L or ends with S?
How many strings can be formed using the letters of the word LOTUS if the word neither starts with L nor ends with S?
Find the number of ways of distributing 12 distinct prizes to 10 students?
Find the value of 6!
Find the value of 4! + 5!
Find the value of 3! × 2!
Find the value of n if (n + 1)! = 20(n − 1)!
How many numbers are there between 99 and 1000 having atleast one of their digits 7?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.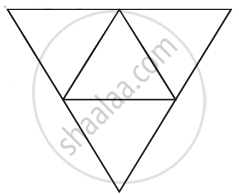
Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements.
A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing question
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the point
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
Find the number of integers greater than 7000 that can be formed with the digits 3, 5, 7, 8 and 9 where no digits are repeated.
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is ______.
The number of six-digit numbers, all digits of which are odd is ______.
There will be only 24 selections containing at least one red ball out of a bag containing 4 red and 5 black balls. It is being given that the balls of the same colour are identical.
