Advertisements
Advertisements
प्रश्न
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
उत्तर
When a coin is tossed once, the number of outcomes is 2 (Head and tail), i.e., in each throw, the number of ways of showing a different face is 2.
Thus, by multiplication principle, the required number of possible outcomes is 2 × 2 × 2 = 8
APPEARS IN
संबंधित प्रश्न
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is allowed?
How many 3-digit numbers can be formed from the digits 1, 2, 3, 4 and 5 assuming that repetition of the digits is not allowed?
How many 3-digit even numbers can be formed from the digits 1, 2, 3, 4, 5, 6 if the digits can be repeated?
How many 4-letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
How many two-letter words can be formed using letters from the word SPACE, when repetition of letters is not allowed?
How many numbers between 100 and 1000 have 4 in the units place?
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
How many two letter words can be formed using letters from the word SPACE, when repetition of letters is not allowed?
How many three-digit numbers can be formed from the digits 0, 1, 3, 5, 6 if repetitions of digits are not allowed?
How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?
How many words can be formed by writing letters in the word CROWN in different order?
How many two-digit numbers can be formed using 1, 2, 3, 4, 5 without repetition of digits?
Three persons enter into a conference hall in which there are 10 seats. In how many ways they can take their seats?
Given four flags of different colours, how many different signals can be generated if each signal requires the use of three flags, one below the other?
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if repetition of digits allowed
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if the repetition of digits is not allowed
How many three-digit odd numbers can be formed by using the digits 0, 1, 2, 3, 4, 5? if the repetition of digits is not allowed
How many three-digit numbers, which are divisible by 5, can be formed using the digits 0, 1, 2, 3, 4, 5 if repetition of digits are not allowed?
To travel from a place A to place B, there are two different bus routes B1, B2, two different train routes T1, T2 and one air route A1. From place B to place C there is one bus route say B1, two different train routes say T1, T2 and one air route A1. Find the number of routes of commuting from place A to place C via place B without using similar mode of transportation
Find the value of 6!
Find the value of 3! × 2!
Find the value of `(12!)/(9! xx 3!)`
Evaluate `("n"!)/("r"!("n" - "r")!)` when for any n with r = 2
Find the value of n if (n + 1)! = 20(n − 1)!
Choose the correct alternative:
In an examination there are three multiple choice questions and each question has 5 choices. Number of ways in which a student can fail to get all answer correct i
Choose the correct alternative:
The number of five digit telephone numbers having at least one of their digits repeated i
Choose the correct alternative:
The number of 10 digit number that can be written by using the digits 2 and 3 is
The number of ways in which a garland can be formed by using 10 identical pink flowers and 9 identical white flowers is ______
All the letters of the word PADMAPRIYA are placed at random in a row. The probability that the word PRIY A occurs without getting split is ______
In a class, there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class for a function. In how many ways can the teacher make this selection?
How many numbers are there between 99 and 1000 having atleast one of their digits 7?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.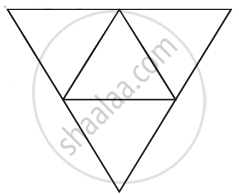
A candidate is required to answer 7 questions out of 12 questions, which are divided into two groups, each containing 6 questions. He is not permitted to attempt more than 5 questions from either group. Find the number of different ways of doing question
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the point
The number of possible outcomes when a coin is tossed 6 times is ______.
The sum of the digits in unit place of all the numbers formed with the help of 3, 4, 5 and 6 taken all at a time is ______.
