Advertisements
Advertisements
प्रश्न
Out of 18 points in a plane, no three are in the same line except five points which are collinear. Find the number of lines that can be formed joining the point
उत्तर
Total number of points = 18
Out of 18 numbers, 5 are collinear and we get a straight line by joining any two points.
∴ Total number of straight-line formed by joining 2 points out of 18 points = 18C2.
Number of straight lines formed by joining 2 points out of 5 points = 5C2
But 5 points are collinear and we get only one line when they are joined pairwise.
So, the required number of straight lines are
= 18C2 – 5C2 + 1
= `(18 * 17)/(2*1) - (5*4)/(2*1) + 1`
= 153 – 10 + 1
= 144
Hence, the total number of straight lines = 144.T
APPEARS IN
संबंधित प्रश्न
A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?
How many two-letter words can be formed using letters from the word SPACE, when repetition of letters is not allowed?
How many numbers between 100 and 1000 have the digit 7 exactly once?
A Signal is generated from 2 flags by putting one flag above the other. If 4 flags of different colours are available, how many different signals can be generated?
In a test, 5 questions are of the form 'state, true or false'. No student has got all answers correct. Also, the answer of every student is different. Find the number of students appeared for the test.
How many numbers between 100 and 1000 have 4 in the units place?
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 5 if digits are not repeated?
Select the correct answer from the given alternatives.
A college has 7 courses in the morning and 3 in the evening. The possible number of choices with the student if he wants to study one course in the morning and one in the evening is -
How many two-digit numbers can be formed using 1, 2, 3, 4, 5 without repetition of digits?
Four children are running a race:
In how many ways can the first two places be filled?
Count the number of three-digit numbers which can be formed from the digits 2, 4, 6, 8 if repetitions of digits is not allowed
How many three-digit numbers are there with 3 in the unit place?
with repetition
How many numbers are there between 100 and 500 with the digits 0, 1, 2, 3, 4, 5? if repetition of digits allowed
How many numbers are there between 1 and 1000 (both inclusive) which are divisible neither by 2 nor by 5?
Find the number of ways of distributing 12 distinct prizes to 10 students?
Find the value of 6!
Find the value of `(12!)/(9! xx 3!)`
Find the value of `(("n" + 3)!)/(("n" + 1)!)`
Evaluate `("n"!)/("r"!("n" - "r")!)` when n = 6, r = 2
Choose the correct alternative:
The number of 5 digit numbers all digits of which are odd i
In a class, there are 27 boys and 14 girls. The teacher wants to select 1 boy and 1 girl to represent the class for a function. In how many ways can the teacher make this selection?
In how many ways can this diagram be coloured subject to the following two conditions?
(i) Each of the smaller triangle is to be painted with one of three colours: red, blue or green.
(ii) No two adjacent regions have the same colour.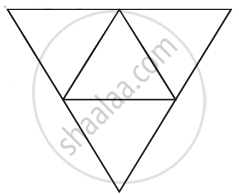
Eight chairs are numbered 1 to 8. Two women and 3 men wish to occupy one chair each. First the women choose the chairs from amongst the chairs 1 to 4 and then men select from the remaining chairs. Find the total number of possible arrangements.
Find the number of positive integers greater than 6000 and less than 7000 which are divisible by 5, provided that no digit is to be repeated.
The number of possible outcomes when a coin is tossed 6 times is ______.
The number of different four-digit numbers that can be formed with the digits 2, 3, 4, 7 and using each digit only once is ______.
The number of six-digit numbers, all digits of which are odd is ______.
