Advertisements
Advertisements
प्रश्न
How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?
उत्तर
A three-digit number is to be formed from the digits 2, 3, 4, 5, 6 where digits can be repeated.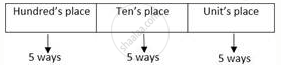
Here, all the places can be filled in 5 ways each.
∴ By using the fundamental principle of multiplication, the total number of three-digit numbers = 5 × 5 × 5 = 125
APPEARS IN
संबंधित प्रश्न
How many five-digit numbers formed using the digit 0, 1, 2, 3, 4, 5 are divisible by 3 if digits are not repeated?
Evaluate: 8!
Evaluate: 6!
Evaluate: 8! – 6!
Compute: `(12/6)!`
Compute: (3 × 2)!
Compute: 3! × 2!
Compute: `(8!)/(6! - 4!)`
Compute: `(8!)/((6 - 4)!)`
Write in terms of factorial:
5 × 6 × 7 × 8 × 9 × 10
Write in terms of factorial:
5 × 10 × 15 × 20 × 25
Evaluate: `("n"!)/("r"!("n" - "r"!)` For n = 12, r = 12
Find n if: `("n"!)/(3!("n" - 3)!) : ("n"!)/(5!("n" - 5)!)` = 5:3
Show that
`("n"!)/("r"!("n" - "r")!) + ("n"!)/(("r" - 1)!("n" - "r" + 1)!) = (("n" + 1)!)/("r"!("n" - "r" + 1)!`
Show that: `(9!)/(3!6!) + (9!)/(4!5!) = (10!)/(4!6!)`
Find the value of: `(8! + 5(4!))/(4! - 12)`
Find the value of: `(5(26!) + (27!))/(4(27!) - 8(26!)`
Five balls are to be placed in three boxes, where each box can contain up to five balls. Find the number of ways if no box is to remain empty.
A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.
