Advertisements
Advertisements
Question
How many three-digit numbers can be formed using the digits 2, 3, 4, 5, 6 if digits can be repeated?
Solution
A three-digit number is to be formed from the digits 2, 3, 4, 5, 6 where digits can be repeated.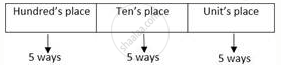
Here, all the places can be filled in 5 ways each.
∴ By using the fundamental principle of multiplication, the total number of three-digit numbers = 5 × 5 × 5 = 125
APPEARS IN
RELATED QUESTIONS
A teacher wants to select the class monitor in a class of 30 boys and 20 girls. In how many ways can he select a student if the monitor can be a boy or a girl?
A teacher wants to select the class monitor in a class of 30 boys and 20 girls, in how many ways can the monitor be selected if the monitor must be a boy? What is the answer if the monitor must be a girl?
Evaluate: (8 – 6)!
Compute: `(12/6)!`
Compute: (3 × 2)!
Compute: `(6! - 4!)/(4!)`
Write in terms of factorial:
6 × 7 × 8 × 9
Find n, if `"n"/(8!) = 3/(6!) + 1/(4!)`
Find n, if `"n"/(6!) = 4/(8!) + 3/(6!)`
Find n, if (n + 1)! = 42 × (n – 1)!
Find n, if (n + 3)! = 110 × (n + 1)!
Find n if: `("n"!)/(3!("n" - 3)!) : ("n"!)/(5!("n" - 5)!)` = 5:3
Find n, if: `((17 - "n")!)/((14 - "n")!)` = 5!
Find n, if: `((2"n")!)/(7!(2"n" - 7)!) : ("n"!)/(4!("n" - 4)!)` = 24:1
Five balls are to be placed in three boxes, where each box can contain up to five balls. Find the number of ways if no box is to remain empty.
A hall has 12 lamps and every lamp can be switched on independently. Find the number of ways of illuminating the hall.
How many quadratic equations can be formed using numbers from 0, 2, 4, 5 as coefficient if a coefficient can be repeated in an equation.
A question paper has 6 questions. How many ways does a student have if he wants to solve at least one question?
