Advertisements
Advertisements
प्रश्न
If a, b, c are all non-zero and a + b + c = 0, prove that `a^2/(bc) + b^2/(ca) + c^2/(ab) = 3`.
उत्तर
To prove, `a^2/(bc) + b^2/(ca) + c^2/(ab) = 3`
We know that, a3 + b3 + c3 – 3abc = (a + b + c)(a2 + b2 + c2 – ab – bc – ca)
= 0(a2 + b2 + c2 – ab – bc – ca) ...[∵ a + b + c = 0, given]
= 0
⇒ a3 + b3 + c3 = 3abc
On dividing both sides by abc, we get
`a^3/(abc) + b^3/(abc) + c^3/(abc) = 3`
⇒ `a^2/(bc) + b^2/(ac) + c^2/(ab) = 3`
Hence proved.
APPEARS IN
संबंधित प्रश्न
Find the value of the polynomial 5x – 4x2 + 3 at x = 0.
Find p(0), p(1) and p(2) for the following polynomial:-
p(x) = x3
Find the zero of the polynomial in the following case:
p(x) = 3x – 2
Find the zero of the polynomial in the following case:
p(x) = 3x
Find the zero of the polynomial in the following case:
p(x) = cx + d, c ≠ 0, c, d are real numbers.
Verify whether the indicated numbers is zeroes of the polynomials corresponding to them in the following case:
`f ( x) = x^2and x = 0`
Find the number of zeros of the following polynomial represented by their graph
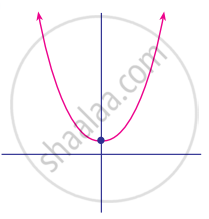
Find the number of zeros of the following polynomial represented by their graph
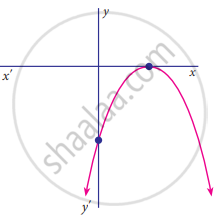
Zero of a polynomial is always 0
Find the zeroes of the polynomial in the following:
h(y) = 2y
