Advertisements
Advertisements
प्रश्न
If D and E are the midpoints of the sides AB and AC of a triangle ABC, prove that `vec"BE" + vec"DC" = 3/2vec"BC"`
उत्तर
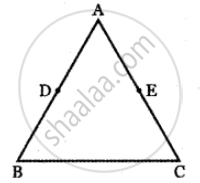
Let O be the origin.
Let `vec"a", vec"b", vec"c"` the position vectors of the points A, B and C respectively
Then `vec"OA" = vec"a", vec"OB" = vec"b", vec"OC" = vec"c"`
Given D is the midpoint of AB
∴ `vec"OD" = (vec"OA" + vec"OB")/2`
`vec"OD" = (vec"a" + vec"b")/2`
Also given E is the midpoint of AC
∴ `vec"OE" = (vec"OA" + vec"OC")/2`
`vec"OE" = (vec"a" + vec"c")/2`
`vec"BE" = vec"OE" - vec"OB"`
= `(vec"a" + vec"c")/2 - vec"b"`
`vec"BE" = (vec"a" + vec"c" - 2vec"b")/2`
`vec"DC" = vec"OC" - vec"OD"`
= `vec"c" - (vec"a" + vec"b")/2`
`vec"DC" = (2vec"c" + vec"a" - vec"b")/2`
`vec"BE" + vec"DC" = (vec"a" + vec"c" - 2vec"b")/2 + (2vec"c" - vec"a" - vec"b")/2`
= `(vec"a" + vec"c" - 2vec"b" + 2vec"c" - vec"a" - vec"b")/2`
= `(3vec"c" - 3vec"b")/2`
= `3/2(vec"c" - vec"b")`
= `3/2(vec"OC" - vec"OB")`
`vec"BE" + vec"DC" = 3/2vec"BC"`
APPEARS IN
संबंधित प्रश्न
Let `vec"a"` and `vec"b"` be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are `(vec"a" + 2vec"b")/3` and `(vec"b" + 2vec"a")/3`
Prove that the line segment joining the midpoints of two sides of a triangle is parallel to the third side whose length is half of the length of the third side
Prove that the line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram
If `vec"a"` and `vec"b"` represent a side and a diagonal of a parallelogram, find the other sides and the other diagonal
If D is the midpoint of the aide BC of a triangle ABC, prove that `vec"AB" + vec"AC" = 2vec"AD"`
If G is the centroid of a triangle ABC, prove that `vec"GA" + vec"GB" + vec"GC" = vec0`
Let A, B, and C be the vertices of a triangle. Let D, E, and F be the midpoints of the sides BC, CA, and AB respectively. Show that `vec"AD" + vec"BE" + vec"CF" = vec0`
If ABCD is a quadrilateral and E and F are the midpoints of AC and BD respectively, then Prove that `vec"AB" + vec"AD" + vec"CB" + vec"CD" = 4vec"EF"`
The position vectors of the vertices of a triangle are `hat"i" + 2hat"j" + 3hat"k", 3hat"i" - 4hat"j" + 5hat"k"` and `-2hat"i" + 3hat"j" - 7hat"k"`. Find the perimeter of the triangle
Show that the points A(1, 1, 1), B(1, 2, 3) and C(2, – 1, 1) are vertices of an isosceles triangle
Choose the correct alternative:
If `vec"r" = (9vec"a" + 7vec"b")/16`, then the point P whose position vector `vec"r"` divides the line joining the points with position vectors `vec"a"` and `vec"b"` in the ratio
Choose the correct alternative:
Two vertices of a triangle have position vectors `3hat"i" + 4hat"j" - 4hat"k"` and `2hat"i" + 3hat"j" + 4hat"k"`. If the position vector of the centroid is `hat"i" + 2hat"j" + 3hat"k"`, then the position vector of the third vertex is
