Advertisements
Advertisements
प्रश्न
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
उत्तर
The slope of the line AB is
After rotation of the line through 15°
The slope of the line AC in new position is tan 60° = 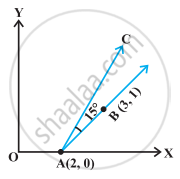
Therefore, the equation of the new line AC is
y – 0 =
or
APPEARS IN
संबंधित प्रश्न
The base of an equilateral triangle with side 2a lies along they y-axis such that the mid point of the base is at the origin. Find vertices of the triangle.
If three point (h, 0), (a, b) and (0, k) lie on a line, show that
Find the slope of the lines which make the following angle with the positive direction of x-axis:
Find the slope of a line passing through the following point:
Find the slope of a line passing through the following point:
(3, −5), and (1, 2)
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
What can be said regarding a line if its slope is zero ?
What can be said regarding a line if its slope is negative?
Show that the line joining (2, −5) and (−2, 5) is perpendicular to the line joining (6, 3) and (1, 1).
The slope of a line is double of the slope of another line. If tangents of the angle between them is
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Line through the points (−2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24). Find the value of x.
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
Find the angle between X-axis and the line joining the points (3, −1) and (4, −2).
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equation of the perpendicular to the line segment joining (4, 3) and (−1, 1) if it cuts off an intercept −3 from y-axis.
Find the angles between the following pair of straight lines:
3x + 4y − 7 = 0 and 4x − 3y + 5 = 0
Find the angles between the following pair of straight lines:
(m2 − mn) y = (mn + n2) x + n3 and (mn + m2) y = (mn − n2) x + m3.
If θ is the angle which the straight line joining the points (x1, y1) and (x2, y2) subtends at the origin, prove that
The reflection of the point (4, – 13) about the line 5x + y + 6 = 0 is ______.
P1, P2 are points on either of the two lines
If p is the length of perpendicular from the origin on the line
The point (4, 1) undergoes the following two successive transformations:
(i) Reflection about the line y = x
(ii) Translation through a distance 2 units along the positive x-axis Then the final coordinates of the point are ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
The line which passes through the origin and intersect the two lines
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is ______.
