Advertisements
Advertisements
Question
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
Solution
The slope of the line AB is `(1 - 0)/(3 - 2)` = 1 or tan 45° (Why?)
After rotation of the line through 15°
The slope of the line AC in new position is tan 60° = `sqrt(3)`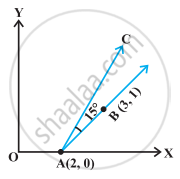
Therefore, the equation of the new line AC is
y – 0 = `sqrt(3) (x - 2)`
or `y - sqrt(3)x + 2sqrt(3)` = 0
APPEARS IN
RELATED QUESTIONS
A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
Find the equation of the lines through the point (3, 2) which make an angle of 45° with the line x –2y = 3.
Find the slope of a line passing through the following point:
(−3, 2) and (1, 4)
Find the slope of a line passing through the following point:
(3, −5), and (1, 2)
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (5, 6) and (2, 3); through (9, −2) and (6, −5)
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
What can be said regarding a line if its slope is zero ?
What can be said regarding a line if its slope is negative?
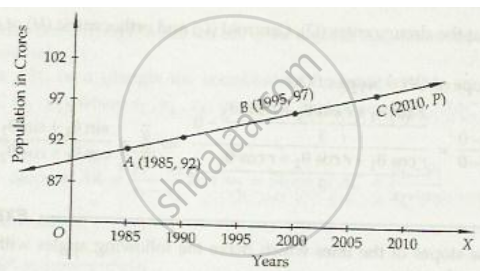
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
Find the equation of a straight line with slope −2 and intersecting the x-axis at a distance of 3 units to the left of origin.
The line through (h, 3) and (4, 1) intersects the line 7x − 9y − 19 = 0 at right angle. Find the value of h.
Find the image of the point (3, 8) with respect to the line x + 3y = 7 assuming the line to be a plane mirror.
Find the angles between the following pair of straight lines:
(m2 − mn) y = (mn + n2) x + n3 and (mn + m2) y = (mn − n2) x + m3.
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
If x + y = k is normal to y2 = 12x, then k is ______.
Point of the curve y2 = 3(x – 2) at which the normal is parallel to the line 2y + 4x + 5 = 0 is ______.
Find the equation of the straight line passing through (1, 2) and perpendicular to the line x + y + 7 = 0.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
The two lines ax + by = c and a′x + b′y = c′ are perpendicular if ______.
The equation of the line passing through (1, 2) and perpendicular to x + y + 7 = 0 is ______.
Find the angle between the lines y = `(2 - sqrt(3)) (x + 5)` and y = `(2 + sqrt(3))(x - 7)`
Find the equation of one of the sides of an isosceles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
The coordinates of the foot of perpendiculars from the point (2, 3) on the line y = 3x + 4 is given by ______.
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is ______.
