Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F.
Find the length of CF.
उत्तर
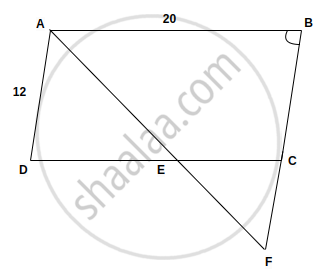
Given AB = 20 cm and AD = 12 cm.
∠DAE = ∠BAF = x and
∠DAE = ∠AFB = x
In ΔABF
∠BAF = ∠BFA
Hence, ABF is an isosceles triangle
So AB = BF = 20
BF = 20
∠ADE = ∠ABF
∴ AD = BC = 12
BC + CF = 20
12 + CF = 20
CF = 20 - 12
CF = 8 cm
APPEARS IN
संबंधित प्रश्न
Two alternate sides of a regular polygon, when produced, meet at the right angle.
Find:
(i)The value of each exterior angle of the polygon;
(ii) The number of sides in the polygon.
The difference between an exterior angle of (n - 1) sided regular polygon and an exterior angle of (n + 2) sided regular polygon is 6° find the value of n.
The ratio between an exterior angle and an interior angle of a regular polygon is 2 : 3. Find the number of sides in the polygon.
AB, BC, and CD are the three consecutive sides of a regular polygon. If BAC = 15°;
Find:
- Each interior angle of the polygon.
- Each exterior angle of the polygon.
- The number of sides of the polygon.
Find each exterior angle of a regular polygon of: 9 sides
Find the number of sides in a regular polygon, when each interior angle is: 120°
Is it possible to have a polygon whose sum of interior angles is 7 right angles?
KL, LM and MN are three consecutive sides of a regular polygon. If ∠LKM = 20°, find the interior angle of the polygon and the number of sides of the polygon.
Find the value of each angle of an octagon if four of its angles are equal and the other four are each greater than these by 20°.
Each exterior angle of a regular polygon is `(1)/"P" `times of its interior angle. Find the number of sides in the polygon.
