Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, AB = 20 cm and AD = 12 cm. The bisector of angle A meets DC at E and BC produced at F.
Find the length of CF.
उत्तर
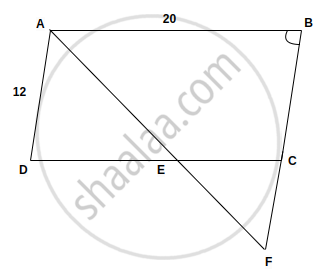
Given AB = 20 cm and AD = 12 cm.
∠DAE = ∠BAF = x and
∠DAE = ∠AFB = x
In ΔABF
∠BAF = ∠BFA
Hence, ABF is an isosceles triangle
So AB = BF = 20
BF = 20
∠ADE = ∠ABF
∴ AD = BC = 12
BC + CF = 20
12 + CF = 20
CF = 20 - 12
CF = 8 cm
APPEARS IN
संबंधित प्रश्न
Two alternate sides of a regular polygon, when produced, meet at the right angle.
Find:
(i)The value of each exterior angle of the polygon;
(ii) The number of sides in the polygon.
Three angles of a seven-sided polygon are 132o each and the remaining four angles are equal. Find the value of each equal angle.
Two angles of an eight-sided polygon are 142o and 176o. If the remaining angles are equal to each other; find the magnitude of each of the equal angles.
Find the number of sides in a regular polygon, when each interior angle is: 135°
Find the number of sides in a regular polygon, when each exterior angle is: 60°
Is it possible to have a polygon whose sum of interior angles is 780°?
Is it possible to have a polygon whose each interior angle is 105°?
KL, LM and MN are three consecutive sides of a regular polygon. If ∠LKM = 20°, find the interior angle of the polygon and the number of sides of the polygon.
The number angle of a regular polygon is double the exterior angle. Find the number of sides of the polygon.
Each exterior angle of a regular polygon is `(1)/"P" `times of its interior angle. Find the number of sides in the polygon.
