Advertisements
Advertisements
प्रश्न
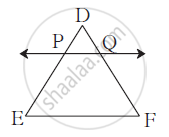
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
उत्तर
In Δ DEF,
line PQ || side EF
∴ `("DP")/("PE") = ("DQ")/("QF")` (∵ Basic proportionality Theoram)
∴ `2.4/7.2= 1/("QF")`
∴ `"QF" xx 2.4 = 7.2`
∴ QF = `7.2/2.4`
∴ QF = 3
APPEARS IN
संबंधित प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
Find the slope and y-intercept of the line:
y = 4
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
Find the equation of the line which is perpendicular to the line `x/a - y/b = 1` at the point where this line meets y-axis.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
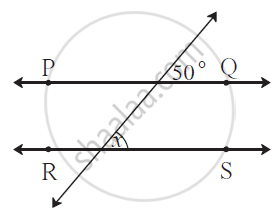
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
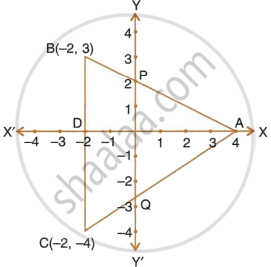
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
