Advertisements
Advertisements
प्रश्न
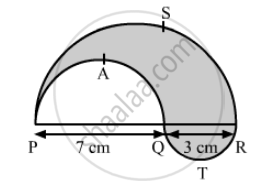
In the the following figure, PSR, RTQ and PAQ are three semicircles of diameter 10 cm, 3 cm and 7 cm respectively. Find the perimeter of shaded region.
उत्तर
Perimeter of shaded region = Length of the arc PAQ + Length of the arc PSR + Length of the arc RTQ
\[= \frac{1}{2} \times 2\pi r_1 + \frac{1}{2} \times 2\pi r_2 + \frac{1}{2} \times 2\pi r_3 \]
\[ = \frac{1}{2} \times 2\pi\left( \frac{7}{2} \right) + \frac{1}{2} \times 2\pi\left( \frac{10}{2} \right) + \frac{1}{2} \times 2\pi\left( \frac{3}{2} \right)\]
\[ = \frac{7}{2}\pi + 5\pi + \frac{3}{2}\pi\]
\[ = 10\pi\]
\[ = 31 . 4 cm\]
Hence, the perimeter of shaded region is 31.4 cm.
APPEARS IN
संबंधित प्रश्न
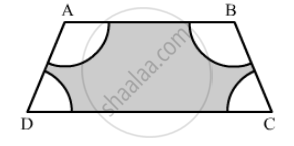
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm DC = 32 cm and the distance between AB and DC is 14 cm. Circles of equal radii 7 cm with centres A, B, C and D have been drawn. Then find the area of the shaded region.
(Use \[\pi = \frac{22}{7}\]
The area of the incircle of an equilateral triangle of side 42 cm is
If the sum of the areas of two circles with radii r1 and r2 is equal to the area of a circle of radius r, then \[r_1^2 + r_2^2\]
A sector is cut from a circle of radius 21 cm. The angle of the sector is 150°. Find the length of the arc and the area of the sector.
The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.
The minute hand of a clock is 12 cm long. Find the area swept by in it 35 minutes.
Find the area of the shaded portion in each of the following diagrams:
(i)

(ii)

Perimeter of a sector of a circle whose central angle is 90° and radius 7 cm is ____________.
A circular park is surrounded by a road 21 m wide. If the radius of the park is 105 m, find the area of the road.
If the radius of a circle is tripled, the area becomes ______.
