Advertisements
Advertisements
प्रश्न
In the given figure, a rocket is fired vertically upwards from its launching pad P. It first rises 20 km vertically upwards and then 20 km at 60° to the vertical. PQ represents the first stage of the journey and QR the second. S is a point vertically below R on the horizontal level as P, find:
a. the height of the rocket when it is at point R.
b. the horizontal distance of point S from P.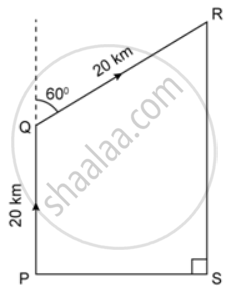
उत्तर
Draw QM ⊥ RS.
Clearly, ∠RQM = 30° 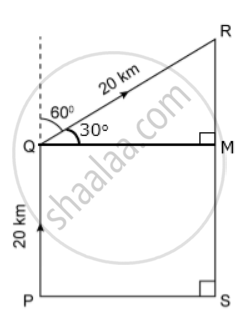
a. In right ΔRMQ,
sin30° = `"RM"/"RQ"`
⇒ `(1)/(2) = "RM"/(20)`
⇒ RM = 10km
∴ The height of the rocket when it is at point R
= RS
= RM + MS
= 10km + 20km
= 30km.
b. In right ΔRMQ,
cos30° = `"QM"/"RQ"`
⇒ `sqrt(3)/(2) = "QM"/(20)`
⇒ QM = `10sqrt(3)"km"`
∴ The horizontal distance of point S from P
=PS
= QM
= `10sqrt(3)"km"`.
APPEARS IN
संबंधित प्रश्न
Solve for x : 2 cos 3x - 1 = 0
Solve the following equation for A, if sec 2A = 2
Solve for x : sin (x + 10°) = `(1)/(2)`
Find the value of 'A', if cosec 3A = `(2)/sqrt(3)`
If tanθ= cotθ and 0°≤ θ ≤ 90°, find the value of 'θ'.
Find the value of 'x' in each of the following: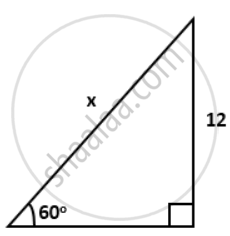
Find:
a. BC
b. AD
c. AC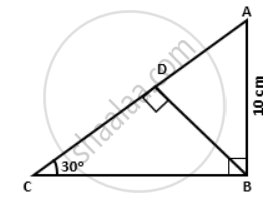
Find the value 'x', if:
Evaluate the following: sin22° cos44° - sin46° cos68°
Evaluate the following: `(5cot5° cot15° cot25° cot35° cot45°)/(7tan45° tan55° tan65° tan75° tan85°) + (2"cosec"12° "cosec"24° cos78° cos66°)/(7sin14° sin23° sec76° sec67°)`
