Advertisements
Advertisements
प्रश्न
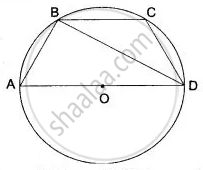
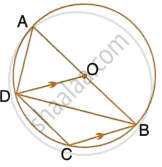
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate:
- ∠DAB,
- ∠DBA,
- ∠DBC,
- ∠ADC.
Also, show that the ΔAOD is an equilateral triangle.
उत्तर

i. ABCD is a cyclic quadrilateral
∴ ∠DCB + ∠DAB = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠DAB = 180° – 120° = 60°
ii. ∠ADB = 90°
(Angle in a semicircle is a right angle)
∴ ∠DBA = 90° – ∠DAB
= 90° – 60°
= 30°
iii. OD = OB
∴ ∠ODB = ∠OBD
Or ∠ABD = 30°
Also, AB || ED
∴ ∠DBC = ∠ODB = 30° (Alternate angles)
iv. ∠ABD + ∠DBC = 30° + 30° = 60°
`=>` ∠ABC = 60°
In cyclic quadrilateral ABCD,
∠ADC + ∠ABC = 180°
(Pair of opposite angles in a cyclic quadrilateral are supplementary)
`=>` ∠ADC = 180° – 60° = 120°
In ∆AOD, OA = OD (Radii of the same circle)
∠AOD = ∠DAO Or ∠DAB = 60° [Proved in (i)]
`=>` ∠AOD = 60°
∠ADO = ∠AOD =∠DAO = 60°
∴ ∆AOD is an equilateral triangle.
APPEARS IN
संबंधित प्रश्न
ABC is a right angles triangle with AB = 12 cm and AC = 13 cm. A circle, with centre O, has been inscribed inside the triangle.
Calculate the value of x, the radius of the inscribed circle.
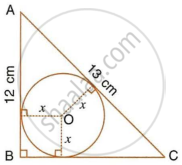
Prove that the perimeter of a right triangle is equal to the sum of the diameter of its incircle and twice the diameter of its circumcircle.
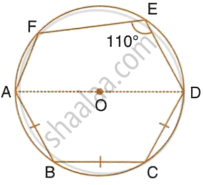
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate: ∠AEF
Prove that the circle drawn on any one of the equal sides of an isosceles triangle as diameter bisects the base.
In the given figure, AB is the diameter of a circle with centre O.
If chord AC = chord AD, prove that:
- arc BC = arc DB
- AB is bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find:
- ∠BAC
- ∠ABC
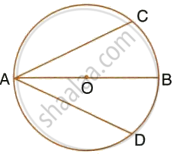
In the given figure, RS is a diameter of the circle. NM is parallel to RS and ∠MRS = 29°. Calculate : ∠NRM
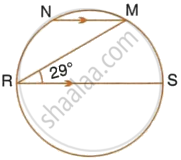
In the given figure, AB is a diameter of the circle. Chord ED is parallel to AB and ∠EAB = 63°. Calculate : ∠BCD.
In the given figure, AB is a diameter of the circle with centre O. DO is parallel to CB and ∠DCB = 120°.
Calculate : ∠DBA
Also, show that the ΔAOD is an equilateral triangle.
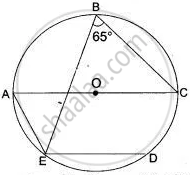
In Fig, Chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, Calculate ∠ DEC.
In the figure given alongside, AD is the diameter of the circle. If ∠ BCD = 130°, Calculate: (i) ∠ DAB (ii) ∠ ADB.