Advertisements
Advertisements
प्रश्न
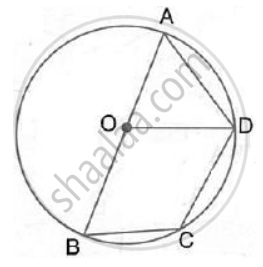
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

उत्तर
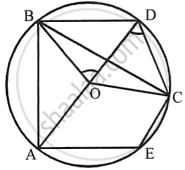
Join BC, BO, CO and EO
Since BD is the side of a regular hexagon,
`∠BOD = 360^circ/6 = 60^circ`
Since DC is the side of a regular pentagon,
`∠COD = 360^circ/5 = 72^circ`
In ∆BOD, ∠BOD = 60° and OB = OD
∴ ∠OBD = ∠ODB = 60°
i. In ∆OCD, ∠COD = 72° and OC = OD
∴ `∠ODC = 1/2 (180^circ - 72^circ)`
= `1/2 xx 108^circ`
= 54°
Or ∠ADC = 54°
ii. ∠BDO = 60° or ∠BDA = 60°
iii. Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
∴ `∠ ABC = 1/2 ∠AOC`
= `1/2 [∠AOD - ∠COD]`
= `1/2 xx (180^circ - 72^circ)`
= `1/2 xx 108^circ`
= 54°
iv. In cyclic quadrilateral AECD
∠AEC + ∠ADC = 180° ...[Sum of opposite angles]
`=>` ∠AEC + 54° = 180°
`=>` ∠AEC = 180° – 54°
`=>` ∠AEC = 126°
APPEARS IN
संबंधित प्रश्न
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
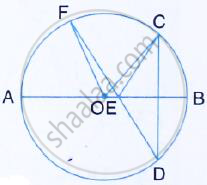
In the figure, O is the centre of the circle, ∠AOE = 150°, ∠DAO = 51°. Calculate the sizes of the angles CEB and OCE.
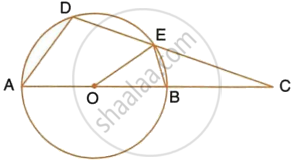
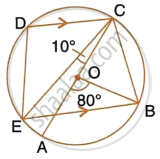
In the given figure, AC is the diameter of the circle with centre O. CD and BE are parallel. Angle ∠AOB = 80° and ∠ACE = 10°.
Calculate:
- Angle BEC,
- Angle BCD,
- Angle CED.
In the given figure, AE is the diameter of the circle. Write down the numerical value of ∠ABC + ∠CDE. Give reasons for your answer.
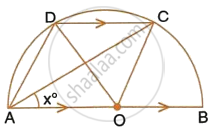
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠CAB = x°; find (in terms of x) the values of :
- ∠COB,
- ∠DOC,
- ∠DAC,
- ∠ADC.
The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon. Find the angles of triangle ABC.

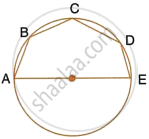
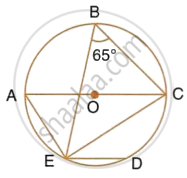
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
AB is the diameter of the circle with centre O. OD is parallel to BC and ∠ AOD = 60° ; calculate the numerical values of: ∠ ADC
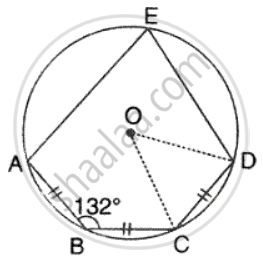
In the given figure, AB = BC = CD and ∠ABC = 132° . Calcualte: ∠ COD.
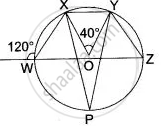
In the figure alongside O is the centre of circle ∠ XOY = 40°, ∠ TWX = 40° and XY is parallel to TZ.
Find: (i) ∠ XZY, (ii) ∠ YXZ (iii) ∠ TZY.