Advertisements
Advertisements
प्रश्न
In the given figure, BD is a side of a regular hexagon, DC is a side of a regular pentagon and AD is a diameter.
Calculate :
- ∠ADC,
- ∠BDA,
- ∠ABC,
- ∠AEC.

उत्तर
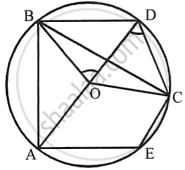
Join BC, BO, CO and EO
Since BD is the side of a regular hexagon,
Since DC is the side of a regular pentagon,
In ∆BOD, ∠BOD = 60° and OB = OD
∴ ∠OBD = ∠ODB = 60°
i. In ∆OCD, ∠COD = 72° and OC = OD
∴
=
= 54°
Or ∠ADC = 54°
ii. ∠BDO = 60° or ∠BDA = 60°
iii. Arc AC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.
∴
=
=
=
= 54°
iv. In cyclic quadrilateral AECD
∠AEC + ∠ADC = 180° ...[Sum of opposite angles]
APPEARS IN
संबंधित प्रश्न
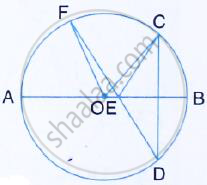
In the figure given below, AB is diameter of the circle whose centre is O. given that: ∠ECD =
∠EDC = 32°. Show that ∠COF = ∠CEF.
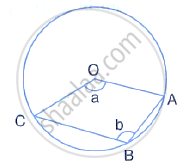
The figure given below, shows a Circle with centre O.
Given: ∠AOC = a and ∠ABC = b.
Find the relationship between a and b
In the given diagram, chord AB = chord BC.
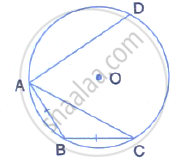
(i) what is the relation between arcs AB and BC?
(ii) what is the relation between ∠AOB and ∠BOC?
(iii) If arc AD is greater than arc ABC, then what is the relation between chords AD and AC?
(iv) If ∠AOB = 50°, find the measure of angle BAC.
In the given figure, AB = BC = CD and ∠ABC = 132°.
Calcualte:
- ∠AEB,
- ∠AED,
- ∠COD.

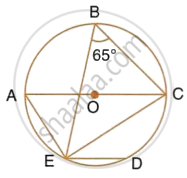
In the given figure, chord ED is parallel to diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.
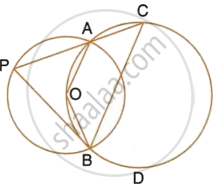
The figure shows two circles which intersect at A and B. The centre of the smaller circle is O and lies on the circumference of the larger circle. Given that ∠APB = a°.
Calculate, in terms of a°, the value of : ∠ADB.
Give reasons for your answers clearly.
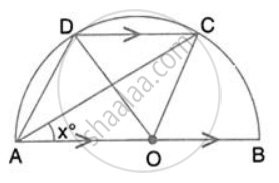
In the given figure, AOB is a diameter and DC is parallel to AB. If ∠ CAB = xo ; find (in terms of x) the values of: ∠ DOC.
In the given figure, the centre O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find : ∠ACB

In a circle with center O, chords AB and CD intersect inside the circumference at E. Prove that ∠ AOC + ∠ BOD = 2∠ AEC.
C is a point on the minor arc AB of the circle, with centre O. Given ∠ACB = x° and ∠AOB = y° express y in terms of x. Calculate x, if ACBO is a parallelogram.
