Advertisements
Advertisements
प्रश्न
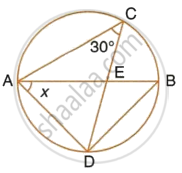
In the given circle with diameter AB, find the value of x.
उत्तर
∠ABD = ∠ACD = 30° ...[Angle in the same segment]
Now in ΔADB,
∠BAD + ∠ADB + ∠ABD = 180° ...[Angles of a triangle]
But, ∠ADB = 90° ...[Angle in a semi-circle]
∴ x + 90° + 30° = 180°
`=>` x + 120° = 180°
`=>` x = 180° – 120°
`=>` x = 60°
APPEARS IN
संबंधित प्रश्न
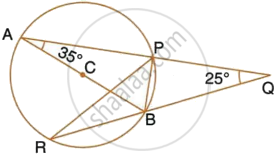
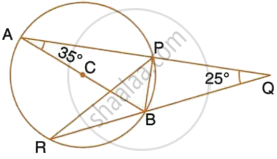
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PRB
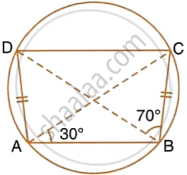
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°.
Find:
- ∠BCD
- ∠BCA
- ∠ABC
- ∠ADB
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in ∠ABC.

AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find : ∠PBR
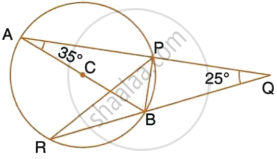
AB is a diameter of the circle APBR, as shown in the figure. APQ and RBQ are straight lines. Find : ∠BPR
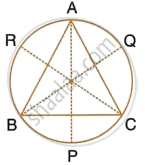
A triangle ABC is inscribed in a circle. The bisectors of angles BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that :
∠ACB = 2∠APR,
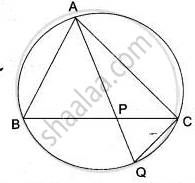
In the given Figure. P is any point on the chord BC of a circle such that AB = AP. Prove that CP = CQ.
In the given below the figure, AB is parallel to DC, ∠BCD = 80° and ∠BAC = 25°, Find
(i) ∠CAD, (ii) ∠CBD, (iii) ∠ADC.

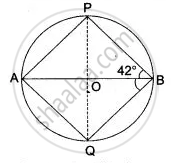
In the following figure, O is the centre of the circle, ∠ PBA = 42°.
Calculate:
(i) ∠ APB
(ii) ∠PQB
(iii) ∠ AQB
In the given figure, ∠CAB = 25°, find ∠BDC, ∠DBA and ∠COB
