Advertisements
Advertisements
प्रश्न
In the given figure, if AB || CD || FE then find x and AE.

उत्तर १
Construction: Join AF intersecting CD at X.
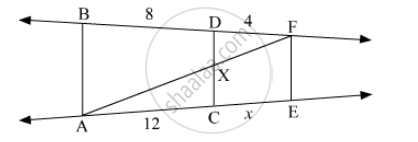
In ΔABF, DX || AB
`"FD"/"DB"="FX"/"XA"` ...(1) (By Basic proportionality theorem)
In ΔAEF, XC || FE
`"FX"/"XA"="EC"/"CA"` ... (2) (By Basic proportionality theorem)
From (1) and (2), we get
`"FD"/"DB"="EC"/"CA"`
`4/8 = x/12`
x = 6
Now, AE = AC + CE
= 12 + 6
= 18
उत्तर २
line AB || line CD || line FE ...(given)
∴ `("BD")/("DF") = ("AC")/("CE")` ...(Property of three parallel lines and their transversals)
∴ `8/4 = 12/x`
∴ x = `(12 xx 4)/8`
∴ x = 6 units
Now, AE = AC + CE [A - C - E]
= 12 + x
= 12 + 6
= 18 units
∴ x = 6 units and AE = 18 units
Notes
Students can refer to the provided solutions based on their preferred marks.
संबंधित प्रश्न
Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

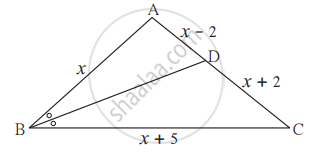
In ∆ABC, seg BD bisects ∠ABC. If AB = x, BC = x + 5, AD = x – 2, DC = x + 2, then find the value of x.
In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find `"AX"/"XY"`.

In Δ ABC and Δ PQR,
∠ ABC ≅ ∠ PQR, seg BD and
seg QS are angle bisector.
`If (l(AD))/(l(PS)) = (l(DC))/(l(SR))`
Prove that : Δ ABC ∼ Δ PQR

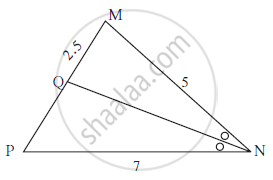
Seg NQ is the bisector of ∠ N
of Δ MNP. If MN= 5, PN =7,
MQ = 2.5 then find QP.
From the top of a light house, an abserver looking at a boat makes an angle of depression of 600. If the height of the lighthouse is 90 m then find how far is the boat from the lighthouse. (3 = 1.73)

In ΔABC, ray BD bisects ∠ABC.
If A – D – C, A – E – B and seg ED || side BC, then prove that:
`("AB")/("BC") = ("AE")/("EB")`
Proof :
In ΔABC, ray BD bisects ∠ABC.
∴ `("AB")/("BC") = (......)/(......)` ......(i) (By angle bisector theorem)
In ΔABC, seg DE || side BC
∴ `("AE")/("EB") = ("AD")/("DC")` ....(ii) `square`
∴ `("AB")/square = square/("EB")` [from (i) and (ii)]
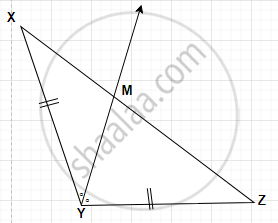
In the figure, ray YM is the bisector of ∠XYZ, where seg XY ≅ seg YZ, find the relation between XM and MZ.
Draw seg AB = 6.8 cm and draw perpendicular bisector of it.
Draw the circumcircle of ΔPMT in which PM = 5.6 cm, ∠P = 60°, ∠M = 70°.
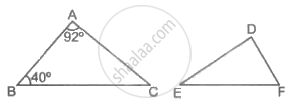
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
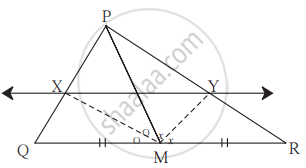
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
Complete the proof by filling in the boxes.
solution:
In ∆PMQ,
Ray MX is the bisector of ∠PMQ.
∴ `("MP")/("MQ") = square/square` .............(I) [Theorem of angle bisector]
Similarly, in ∆PMR, Ray MY is the bisector of ∠PMR.
∴ `("MP")/("MR") = square/square` .............(II) [Theorem of angle bisector]
But `("MP")/("MQ") = ("MP")/("MR")` .............(III) [As M is the midpoint of QR.]
Hence MQ = MR
∴ `("PX")/square = square/("YR")` .............[From (I), (II) and (III)]
∴ XY || QR .............[Converse of basic proportionality theorem]
