Advertisements
Advertisements
प्रश्न
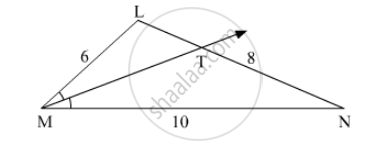
In ∆LMN, ray MT bisects ∠LMN If LM = 6, MN = 10, TN = 8, then Find LT.
उत्तर
\[\text{In} \bigtriangleup \text{LNM}, \]
\[\frac{\text{LT}}{\text{NT}} = \frac{\text{LM}}{\text{NM}} \left( \text{ By angle bisector theorem } \right)\]
\[ \Rightarrow \frac{\text{LT}}{8} = \frac{6}{10}\]
\[\Rightarrow \text{LT} = \frac{8 \times 6}{10}\]
\[ = 4 . 8\]
Hence, the measure of LT is 4.8.
APPEARS IN
संबंधित प्रश्न
Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

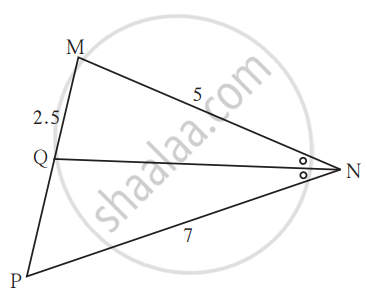
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP.
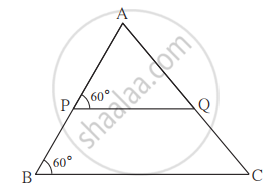
Measures of some angles in the figure are given. Prove that `"AP"/"PB" = "AQ"/"QC"`.
In the given figure, if AB || CD || FE then find x and AE.

In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.

Complete the proof by filling in the boxes.
In △PMQ, ray MX is bisector of ∠PMQ.
∴ `square/square = square/square` .......... (I) theorem of angle bisector.
In △PMR, ray MY is bisector of ∠PMQ.
∴ `square/square = square/square` .......... (II) theorem of angle bisector.
But `(MP)/(MQ) = (MP)/(MR)` .......... M is the midpoint QR, hence MQ = MR.
∴ `(PX)/(XQ) = (PY)/(YR)`
∴ XY || QR .......... converse of basic proportionality theorem.
In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find `"AX"/"XY"`.

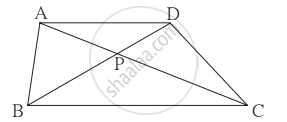
In ▢ABCD, seg AD || seg BC. Diagonal AC and diagonal BD intersect each other in point P. Then show that `"AP"/"PD" = "PC"/"BP"`.
In Δ ABC and Δ PQR,
∠ ABC ≅ ∠ PQR, seg BD and
seg QS are angle bisector.
`If (l(AD))/(l(PS)) = (l(DC))/(l(SR))`
Prove that : Δ ABC ∼ Δ PQR

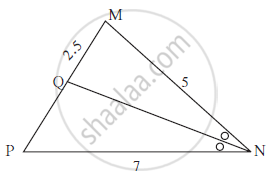
Seg NQ is the bisector of ∠ N
of Δ MNP. If MN= 5, PN =7,
MQ = 2.5 then find QP.
From the top of a light house, an abserver looking at a boat makes an angle of depression of 600. If the height of the lighthouse is 90 m then find how far is the boat from the lighthouse. (3 = 1.73)
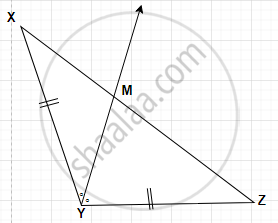
In the figure, ray YM is the bisector of ∠XYZ, where seg XY ≅ seg YZ, find the relation between XM and MZ.
Draw seg AB = 6.8 cm and draw perpendicular bisector of it.
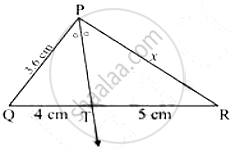
In the following figure, ray PT is the bisector of ∠QPR Find the value of x and perimeter of ∠QPR.
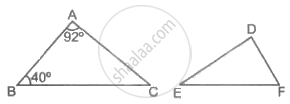
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?
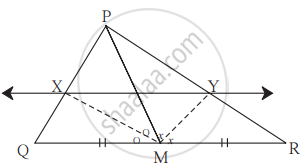
In ∆PQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR intersect side PQ and side PR in points X and Y respectively. Prove that XY || QR.
Complete the proof by filling in the boxes.
solution:
In ∆PMQ,
Ray MX is the bisector of ∠PMQ.
∴ `("MP")/("MQ") = square/square` .............(I) [Theorem of angle bisector]
Similarly, in ∆PMR, Ray MY is the bisector of ∠PMR.
∴ `("MP")/("MR") = square/square` .............(II) [Theorem of angle bisector]
But `("MP")/("MQ") = ("MP")/("MR")` .............(III) [As M is the midpoint of QR.]
Hence MQ = MR
∴ `("PX")/square = square/("YR")` .............[From (I), (II) and (III)]
∴ XY || QR .............[Converse of basic proportionality theorem]
