Advertisements
Advertisements
प्रश्न
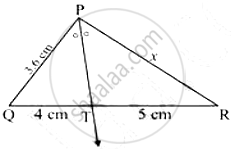
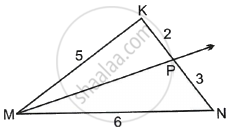
In the following figure, ray PT is the bisector of ∠QPR Find the value of x and perimeter of ∠QPR.
उत्तर
In Δ PQR, PT is the bisector of ∠P
∴ `"QT"/"TR" = "PQ"/"PR"`
⇒ `4/5 = 3.6/"PR"`
⇒ 4PR = 18
⇒PR = `18/4= 9/2 = 4.5`cm
⇒ QR =QT +TR
⇒ QR = 4+5 = 9 cm
⇒ Perimeter of Δ PQR =PQ+QR +PR
⇒ 3.6+9+4.5 = 17.1 cm
⇒ Perimeter of Δ PQR = 17.1 cm
APPEARS IN
संबंधित प्रश्न
Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

Given below is the triangle and length of line segments. Identify in the given figure, ray PM is the bisector of ∠QPR.

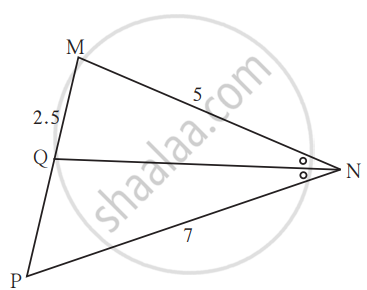
In ∆MNP, NQ is a bisector of ∠N. If MN = 5, PN = 7 MQ = 2.5 then find QP.
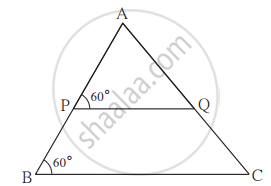
Measures of some angles in the figure are given. Prove that `"AP"/"PB" = "AQ"/"QC"`.
In the given figure, if AB || CD || FE then find x and AE.

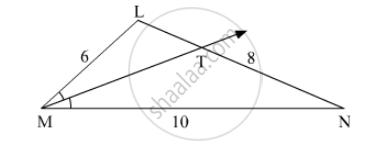
In ∆LMN, ray MT bisects ∠LMN If LM = 6, MN = 10, TN = 8, then Find LT.
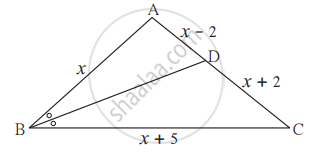
In ∆ABC, seg BD bisects ∠ABC. If AB = x, BC = x + 5, AD = x – 2, DC = x + 2, then find the value of x.
In the given fig, bisectors of ∠B and ∠C of ∆ABC intersect each other in point X. Line AX intersects side BC in point Y. AB = 5, AC = 4, BC = 6 then find `"AX"/"XY"`.

In Δ ABC and Δ PQR,
∠ ABC ≅ ∠ PQR, seg BD and
seg QS are angle bisector.
`If (l(AD))/(l(PS)) = (l(DC))/(l(SR))`
Prove that : Δ ABC ∼ Δ PQR

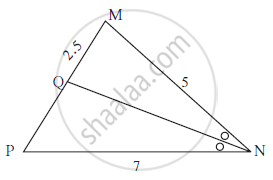
Seg NQ is the bisector of ∠ N
of Δ MNP. If MN= 5, PN =7,
MQ = 2.5 then find QP.
From the top of a light house, an abserver looking at a boat makes an angle of depression of 600. If the height of the lighthouse is 90 m then find how far is the boat from the lighthouse. (3 = 1.73)

In ΔABC, ray BD bisects ∠ABC.
If A – D – C, A – E – B and seg ED || side BC, then prove that:
`("AB")/("BC") = ("AE")/("EB")`
Proof :
In ΔABC, ray BD bisects ∠ABC.
∴ `("AB")/("BC") = (......)/(......)` ......(i) (By angle bisector theorem)
In ΔABC, seg DE || side BC
∴ `("AE")/("EB") = ("AD")/("DC")` ....(ii) `square`
∴ `("AB")/square = square/("EB")` [from (i) and (ii)]
Draw seg AB = 6.8 cm and draw perpendicular bisector of it.
From the information given in the figure, determine whether MP is the bisector of ∠KMN.
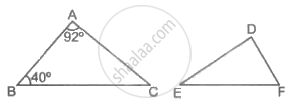
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?

In ΔABC, ray BD bisects ∠ABC, A – D – C, seg DE || side BC, A – E – B, then for showing `("AB")/("BC") = ("AE")/("EB")`, complete the following activity:
Proof :
In ΔABC, ray BD bisects ∠B.
∴ `square/("BC") = ("AD")/("DC")` ...(I) (`square`)
ΔABC, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ...(II) (`square`)
∴ `("AB")/square = square/("EB")` ...[from (I) and (II)]
