Advertisements
Advertisements
प्रश्न
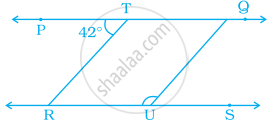
In the given figure, PQ || RS, TR || QU and ∠PTR = 42°. Find ∠QUR.
उत्तर
Since, PQ || RS and TR is a transversal.
∴ ∠PTR – ∠TRU = 42° ......(i) [Alternate interior angles]
Also, TR || QU and RS is a transversal.
∴ ∠TRU + ∠QUR = 180° ......[Co-interior angles]
⇒ 42° + ∠QUR = 180° ......[Using (i)]
⇒ ∠QUR = 180° – 42° = 138°
APPEARS IN
संबंधित प्रश्न
Find the value of angle a in the following figure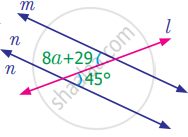
Find the value of angle a in the following figure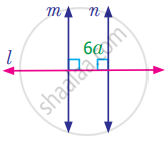
Which of the following statement is ALWAYS TRUE when parallel lines are cut by a transversal
Two parallel lines are cut by a transversal. For each pair of interior angles on the same side of the transversal, if one angle exceeds the twice of the other angle by 48°. Find the angles
In the parking lot shown, the lines that mark the width space are parallel. If ∠1 =(x + 39)°, ∠2 = (2x – 3y)° find x and y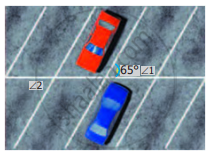
In the figure AB in parallel to CD. Find x°, y° and z°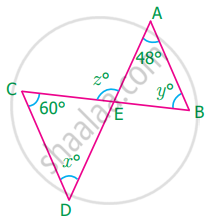
Two parallel lines are cut by transversal. If one angle of a pair of corresponding angles can be represented by 42° less than three times the other. Find the corresponding angles
Anbu has marked the angles as shown in the following figure. Check whether it is correct. Give reason
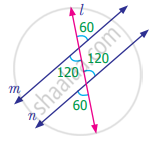
In the given figure, l || m || n. ∠QPS = 35° and ∠QRT = 55°. Find ∠PQR.

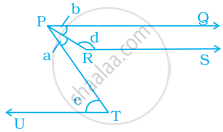
In the given figure, PQ, RS and UT are parallel lines. If c = 57° and a = `c/3`, find the value of d.