Advertisements
Advertisements
प्रश्न
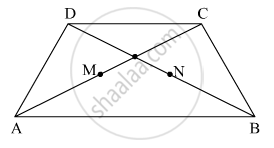
खालील आकृती मध्ये `square`ABCD हा समलंब चौकोन आहे. AB || DC. M आणि N हे अनुक्रमे कर्ण AC व कर्ण DB चे मध्यबिंदू आहेत. तर सिद्ध करा की, MN || AB.
उत्तर
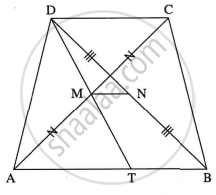
पक्ष: `square`ABCD हा समलंब चौकोन आहे. AB || DC
M आणि N हे अनुक्रमे कर्ण AC व कर्ण DB चे मध्यबिंदू आहेत.
साध्य: MN || AB
रचना: रेख DM अशी काढा की जी बाजू AB ला बिंदु T मध्ये छेदेल.
सिद्धता:
बाजू DC || बाजू AB व रेख AC त्यांची छेदिका आहे.
∴ ∠DAC ≅ ∠BAC ...(व्युत्क्रम कोन)
∴ ∠DCM ≅ ∠TAM ...(i) ...(A-M-C व A-T-B)
∆DCM व ∆TAM मध्ये,
∠DCM ≅ ∠TAM ...[(i) वरून]
रेख MC ≅ रेख MA ...(बिंदु M हा रेख AC चा मध्यबिंदू आहे.)
∠DCM ≅ ∠TAM ...(परस्पर विरुद्ध कोन)
∴ ∆DCM ≅ ∆TAM ...(कोबाको कसोटी)
रेख DM ≅ रेख MT ...(एकरूप त्रिकोणाच्या संगत बाजू) ...(ii)
∆DTB मध्ये,
बिंदु N हा रेख DB चा मध्यबिंदू आहे. ...(पक्ष)
बिंदु M हा रेख DT चा मध्यबिंदू आहे. ...[(ii) वरून]
∴ रेख MN || बाजू TB ...(मध्यबिंदूचे प्रमेय)
∴ रेख MN || रेख AB ...(A-T-B)
APPEARS IN
संबंधित प्रश्न
खालील आकृती मध्ये ΔABC च्या बाजू AB, बाजू BC व बाजू AC चे अनुक्रमे बिंदू X, Y, Z हे मध्यबिंदू आहेत. AB = 5 सेमी, AC = 9 सेमी व BC = 11 सेमी, तर XY, YZ, XZ ची लांबी काढा.

खालील आकृती मध्ये `square`PQRS आणि `square`MNRL हे आयत आहेत. बिंदू M हा PR चा मध्यबिंदू आहे. तर सिद्ध करा.
- SL = LR
- LN = `1/2` SQ

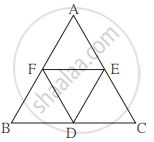
खालील आकृती मध्ये ΔABC या समभुज त्रिकोणात बिंदू F, D, E हे अनुक्रमे बाजू AB, बाजू BC, बाजू AC चे मध्यबिंदू आहेत तर ΔFED हा समभुज त्रिकोण आहे हे सिद्ध करा.
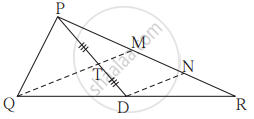
आकृती मध्ये रेख PD ही ΔPQR ची मध्यगा आहे. बिंदू T हा PD चा मध्यबिंदू आहे. QT वाढवल्यावर PR ला M बिंदूत छेदतो, तर दाखवा की `"PR"/"PM" = 1/3`.
[सूचना: DN || QM काढा.]
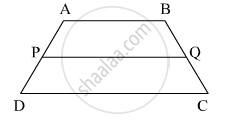
खालील आकृती मध्ये `square`ABCD हा समलंब चौकोन आहे. AB || DC आहे. P व Q हे अनुक्रमे रेख AD व रेख BC चे मध्यबिंदू आहेत, तर सिद्ध करा की, PQ || AB व PQ = `1/2 ("AB" + "DC")`