Advertisements
Advertisements
प्रश्न
किसी निश्चित आधार b के एक समद्विबाहु त्रिभुज की समान भुजाएँ 3 cm/s की दर से घट रही हैं। उस समय जब त्रिभुज की समान भुजाएँ आधार के बराबर हैं, उसका क्षेत्रफल कितनी तेजी से घट रहा है?
उत्तर १
माना ABC एक समद्विबाहु त्रिभुज है। जिसमें AB = AC = x (माना)
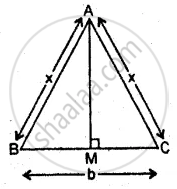
M, BC का मध्य बिन्दु है अर्थात
BM = CM = `b/2`
`AM^2 = AC^2 - MC^2 = x^2 - (b/2)^2`
`= x^2 - b^2/4`
Δ ABC का क्षेत्रफल S = `1/2 xx BC xx AM`
`= 1/2 xx b xx sqrt(x^2 - b^2/4)`
`(dS)/dt = b/2 xx 1/2 xx 1/(sqrt(x^2 - b^2/4)) xx 2x * dx/dt`
`= (bx)/2 xx 2/(sqrt(4x^2 - b^2)) xx dx/dt`
x = b, `dx/dt = 3` रखने पर,
`(dS)/dt = (- 3b * b)/(2 sqrt(b^2 - b^2/4))`
`= (3b)^2/2 * 2/sqrt3b`
`= - sqrt3 b`
त्रिभुज ABC के क्षेत्रफल का ह्रास `sqrt3b` cm2/sec की दर से हो रहा है।
उत्तर २
मान लीजिए कि AB और AC दोनों में से कोई भी बराबर भुजा x है
⇒ `dx/dt = -3` cm/sec.
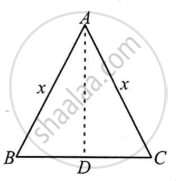
यदि A, ΔABC का संगत क्षेत्रफल है
`A = 1/2` आधार × ऊँचाई = `1/2 b sqrt (AB^2 - BD^2)`
`= b/2 sqrt (x^2 - (b/2)^2)`
`= b/4 sqrt (4x^2 - b^2)`
`(dA)/dt = b/4 xx 1/2 xx (8x)/ sqrt (4x^2 - b^2) dx/dt`
`= (bx)/ sqrt (4x^2 - b^2) dx/dt`
`((dA)/dt)_(x = b) = ((b xxb)/ sqrt (4b^2 - b^2)) (-3)`
`= - sqrt(3b)`
क्षेत्रफल `b sqrt3` cm2/ sec की दर से घट रहा है।
APPEARS IN
संबंधित प्रश्न
एक घन का आयतन 8 cm3/s की दर से बढ़ रहा है। पृष्ठ का क्षेत्रफल किस दर से बढ़ रहा है जब कि इसके किनारे की लंबाई 12 cm हैं।
एक वृत्त की त्रिज्या समान रूप से 3 cm/s की दर से बढ़ रही है। ज्ञात कीजिए की वृत्त का क्षेत्रफल किस दर से बढ़ रहा है जब त्रिज्या 10 cm है।
एक परिवर्तनशील घन का किनारा 3 cm/s की दर से बढ़ रहा है। घन का आयतन किस दर से बढ़ रहा है जबकि किनारा 10 cm लंबा है?
एक स्थिर झील में एक पत्थर डाला जाता है और तरंगें वृत्तों में 5 cm/s की गति से चलती है। जब वृत्ताकार तरंग की त्रिज्या 8 cm है तो उस क्षण, घिरा हुआ क्षेत्रफल किस दर से बढ़ रहा है।
एक वृत्त की त्रिज्या 0.7 cm/s की दर से बढ़ रही है। इसकी परिधि की वृद्धि की दर क्या है जब r = 4.9 cm है?
एक आयत की लंबाई x, 5 cm/min की दर से घट रही है और चौड़ाई y, 4 cm/min की दर से बढ़ रही है। जब x = 8 cm और y = 6 cm है। तब आयत के परिमाप के दर ज्ञात कीजिए।
एक गुब्बारा जो सदैव गोलाकर रहता है, एक पंप द्वारा 900 cm3 गैस प्रति सेकंड भर कर फुलाया जाता है। गुब्बारे की त्रिज्या के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 15 cm है।
एक गुब्बारा जो सदैव गोलाकार रहता है कि त्रिज्या परिवर्तनशील है। त्रिज्या के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए जब त्रिज्या 10 cm है।
एक कण वक्र 6y = x3 + 2 के अनुगत गति कर रहा है। वक्र पर उन बिंदुओं को ज्ञात कीजिए जबकि x निर्देशांक की तुलना में y निर्देशांक 8 गुना तीव्रता से बदल रहा है।
हवा के बुलबुले की त्रिज्या, `1/2` cm/s दर से बढ़ रही है। बुलबुले का आयतन किस दर से बढ़ रहा है जबकि त्रिज्या 1 cm है?
एक गुब्बारा, जो सदैव गोलाकार रहता है, का परिवर्तनशील व्यास `3/2` (2x + 1) है। x के सापेक्ष आयतन के परिवर्तन की दर ज्ञात कीजिए।
एक पाइप से रेत 12 cm3/s की दर से गिर रही है। गिरती रेत जमीन पर एक ऐसा शंकु बनाती है जिसकी ऊँचाई सदैव आधार की त्रिज्या का छठा भाग है। रेत से बने शंकु की ऊँचाई किस दर से बढ़ रही है जबकि ऊँचाई 4 cm है?
एक वस्तु की x इकाइयों के उत्पादन की कुल लागत C (x) (रुपये में) C(x) = 0.007x3 – 0.003x2 + 15x + 4000 से प्राप्त होती है। सीमांत लागत ज्ञात कीजिए जबकि 17 इकाइयों का उत्पादन किया गया है।
किसी उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय R(x) रुपयों में R(x) = 13x2 + 26x + 15 से प्रदत्त है। सीमांत आय ज्ञात कीजिए जब x = 7 है।
एक वृत्त की त्रिज्या r = 6 सेमी पर r के सापेक्ष क्षेत्रफल में परिवर्तन की दर है:
एक उत्पाद की x इकाइयों के विक्रय से प्राप्त कुल आय रुपयों में R(x) = 3x2 + 36x + 5 से प्रदत्त है। जब x = 15 है तो सीमांते आये है:
वृत्त के क्षेत्रफल के परिवर्तन की दर इसकी त्रिज्या के सापेक्ष ज्ञात कीजिए जबकि r = 3 cm है।
वक्र x2 = 4y के बिन्दु (1, 2) पर अभिलम्ब का समीकरण ज्ञात कीजिए।
