Question

किसी त्रिभुज के शीर्षबिंदु A(-3,1), B(0,-2) और C(1,3) हों तो इस त्रिभुज के परिकेंद्र के निर्देशांक ज्ञात कीजिए।

Answer 1

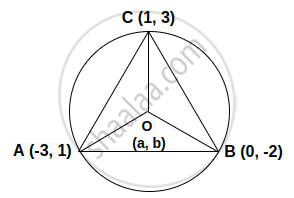
मानो कि, A(-3, 1); B(0, -2); C(1, 3) और परिकेंद्र O(a, b) है |

OA = OC .............(एक ही वृत्त की त्रिज्याएँ)

∴ `sqrt([(a - (-3))]^2 + (b - 1)^2) = sqrt((a - 1)^2 + (b - 3)^2)` ...............(दूरी सूत्र से)

दोनों पक्षों का वर्गमूल लेने पर,

(a + 3)² + (b - 1)² = (a - 1)² + (b - 3)²

∴ a² + 6a + 9 + b² - 2b + 1 = a² - 2a + 1 + b² - 6b + 9 

∴ 6a - 2b = -2a - 6b

∴ 6a + 2a = -6b + 2b

∴ 8a = -4b

∴ 8a = -4b

∴ 8a + 4b = 0

∴ 4(2a + b) = 0

दोनों पक्षों में 4 से भाग देने पर,

∴ 2a + b = 0 ................(1)

OB = OC .................(एक ही वृत्त की त्रिज्याएँ)

∴ `sqrt((a - 0)^2 + [(b - (-2))]^2 = sqrt((a - 1)^2 + (b - 3)^2)` .............(दूरी सूत्र से)

दोनों पक्षों का वर्गमूल लेने पर,

(a - 0)² + (b + 2)² = (a - 1)² + (b - 3)²

∴ `a^2 + b^2 + 4b + 4 = a^2 - 2a + 1 + b^2 - 6a + 9`

∴ 4b + 4 = -2a - 6b + 10

∴ 2a + 4b + 6b = 10 - 4

∴ 2a + 10b = 6

∴ 2(a + 5b) = 6

∴ a + 5b = `6/2`

∴ a + 5b = 3 .................(2)

समीकरण (2) के दोनों पक्षों में 2 से गुणा करने पर,

2a +  10b = 6 .....................(3)

समीकरण (3) में से समीकरण (1) को घटाने पर,

2a + 10b = 6
2a +  b    = 0
-    -        -      
         9b = 6

∴ b = `6/9`

∴ b = `2/3`

b का मान समीकरण (1) में रखने पर,

2a + b = 0

∴ `2a + 2/3 = 0`

∴ 2a = `(-2)/3`

∴ `a = (-2)/3 xx 1/2`

∴ a = `(-1)/3`

त्रिभुज के परिकेंद्र का निर्देशांक `underline(((-1)/3, 2/3)` है |