Advertisements
Advertisements
प्रश्न
एक वृत्त का केंद्र मूलबिंदु पर है तथा एक बिंदु P(5, 0) इस वृत्त पर स्थित है। बिंदु Q(6, 8) इस वृत्त के बाहर स्थित है।
पर्याय
सत्य
असत्य
Advertisements
उत्तर
यह कथन सत्य है।
स्पष्टीकरण:
सबसे पहले, हम दी गई जानकारी से एक वृत्त और एक बिंदु बनाते हैं।
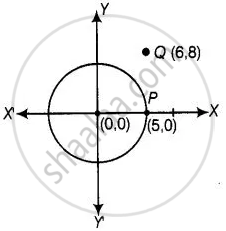
अब, मूल बिन्दु अर्थात् O(0, 0) और P(5, 0) के बीच की दूरी,
OP = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
OP = `sqrt((5 - 0)^2 + (0 - 0)^2`
= `sqrt(5^2 + 0^2)`
= 5
= वृत्त की त्रिज्या और मूल बिंदु O(0, 0) और Q(6, 8) के बीच की दूरी,
OQ = `sqrt((6 - 0)^2 + (8 - 0)^2`
= `sqrt(6^2 + 8^2)`
= `sqrt(36 + 64)`
= `sqrt(100)`
= 10
हम जानते हैं कि, यदि केंद्र से किसी बिंदु की दूरी त्रिज्या से कम/बराबर/अधिक है, तो वह बिंदु क्रमशः वृत्त के अंदर/पर/बाहर होता है।
यहाँ, हम देखते हैं कि, OQ > OP
अतः, यह सत्य है कि बिंदु Q(6, 8), वृत्त के बाहर स्थित है।
APPEARS IN
संबंधित प्रश्न
सिद्ध कीजिए कि, A(1, 2), B(1, 6), C(1 + `2sqrt3`, 4) समबाहु त्रिभुज के शीर्ष बिंदु हैं।
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरी ज्ञात कीजिए:
(2, 3), (4, 1)
बिंदुओं (0,0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है?
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x, y) बिंदुओं (3, 6) और (–3, 4) से समदूरस्थ हो।
AOBC एक आयत है, जिसके तीन शीर्ष A(0, 3), O(0, 0) और B(5, 0) हैं। इसका विकर्ण ______ हैं।
तीन शीर्षों A(–2, 3), B(6, 7) और C(8, 3) वाले समांतर चतुर्भुज ABCD का चौथा शीर्ष D ______ हैं।
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
एक बिंदु ज्ञात कीजिए, जो A(–5, 4) और B(–1, 6) से समदूरस्थ हो। ऐसे कितने बिंदु हैं?
यदि (a, b), बिंदुओं A(10, –6) और B(k, 4) को मिलाने वाले रेखाखंड का मध्य-बिंदु है तथा a – 2b = 18 है, तो k का मान और दूरी AB ज्ञात कीजिए।
