Advertisements
Advertisements
प्रश्न
Let X = {a, b, c, d} and R = {(a, a), (b, b), (a, c)}. Write down the minimum number of ordered pairs to be included to R to make it equivalence
उत्तर
Given X = {a, b, c, d}
R = {(a, a), (b, b), (a, c)}
To make R reflexive we need to include (c, c)
To make R symmetric we need to include (c, c) and (c, a) for transitive
∴ The relation now becomes
R = {(a, a), (b, b), (a, c), (c, c), (c, a)}
∴ R is equivalence relation.
APPEARS IN
संबंधित प्रश्न
Let A = {1, 2, 3, …, 14}. Define a relation R from A to A by R = {(x, y): 3x – y = 0, where x, y ∈ A}. Write down its domain, codomain and range.
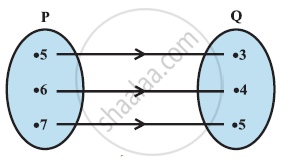
The given figure shows a relationship between the sets P and Q. Write this relation
- in set-builder form.
- in roster form.
What is its domain and range?
Write the relation R = {(x, x3): x is a prime number less than 10} in roster form.
Find the inverse relation R−1 in each of the cases:
(iii) R is a relation from {11, 12, 13} to (8, 10, 12] defined by y = x − 3.
Determine the domain and range of the relations:
(i) R = {(a, b) : a ∈ N, a < 5, b = 4}
Let A = {a, b}. List all relations on A and find their number.
Let R be a relation from N to N defined by R = {(a, b) : a, b ∈ N and a = b2}. Is the statement true?
(a, b) ∈ R implies (b, a) ∈ R
Justify your answer in case.
Let A = [1, 2, 3, ......., 14]. Define a relation on a set A by
R = {(x, y) : 3x − y = 0, where x, y ∈ A}.
Depict this relationship using an arrow diagram. Write down its domain, co-domain and range.
Let R be a relation on N × N defined by
(a, b) R (c, d) ⇔ a + d = b + c for all (a, b), (c, d) ∈ N × N
Show that:
(ii) (a, b) R (c, d) ⇒ (c, d) R (a, b) for all (a, b), (c, d) ∈ N × N
If R is a relation from set A = (11, 12, 13) to set B = (8, 10, 12) defined by y = x − 3, then write R−1.
If A = {1, 2, 4}, B = {2, 4, 5}, C = {2, 5}, then (A − B) × (B − C) is
Let A = {1, 2, 3, 4), B = {4, 5, 6}, C = {5, 6}. Verify, A × (B ∪ C) = (A × B) ∪ (A × C)
Identify which of if the following relations are reflexive, symmetric, and transitive.
| Relation | Reflexive | Symmetric | Transitive |
| R = {(a, b) : a, b ∈ Z, a – b is an integer} | |||
| R = {(a, b) : a, b ∈ N, a + b is even} | √ | √ | x |
| R = {(a, b) : a, b ∈ N, a divides b} | |||
| R = {(a, b) : a, b ∈ N, a2 – 4ab + 3b2 = 0} | |||
| R = {(a, b) : a is sister of b and a, b ∈ G = Set of girls} | |||
| R = {(a, b) : Line a is perpendicular to line b in a plane} | |||
| R = {(a, b) : a, b ∈ R, a < b} | |||
| R = {(a, b) : a, b ∈ R, a ≤ b3} |
Let A = {9, 10, 11, 12, 13, 14, 15, 16, 17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f
Discuss the following relation for reflexivity, symmetricity and transitivity:
On the set of natural numbers the relation R defined by “xRy if x + 2y = 1”
On the set of natural numbers let R be the relation defined by aRb if 2a + 3b = 30. Write down the relation by listing all the pairs. Check whether it is equivalence
On the set of natural numbers let R be the relation defined by aRb if a + b ≤ 6. Write down the relation by listing all the pairs. Check whether it is transitive
Choose the correct alternative:
The number of relations on a set containing 3 elements is
Let S = {x ∈ R : x ≥ 0 and `2|sqrt(x) - 3| + sqrt(x)(sqrt(x) - 6) + 6 = 0}`. Then S ______.
