Advertisements
Advertisements
प्रश्न
Let X be a discrete random variable with the following p.m.f
`"P"(x) = {{:(0.3, "for" x = 3),(0.2, "for" x = 5),(0.3, "for" x = 8),(0.2, "for" x = 10),(0, "otherwise"):}`
Find and plot the c.d.f. of X.
उत्तर
F(3) = P(x ≤ 3)
= P(3)
= 0.3
F(5) = P(x ≤ 5)
= P(x = 3) + (x = 5)
= 0.3 + 0.2
= 0.5
F(8) = P(x ≤ 8)
= P(3) + P(5) + P(8)
= 0.3 + 0.2 + 0.3
= 0.8
F(10) = P(x ≤ 10)
= P(3) + P(5) + P(8) + P(10)
= 0.3 + 0.2 + 0.3 + 0.2
= 1
`"F"_x(x) = {{:(0, "for" x < 3),("P"_x(3) = 0.3, "for" 3 ≤ x < 5),("P"_x(3) + "P"_x(5) = 0.5, "for" 5 ≤ x < 8),("P"_x(3) + "P"_x(5) + "P"_x(8) = 0.8, "for" 8 ≤ x < 10),(1, "for" x ≥ 10):}`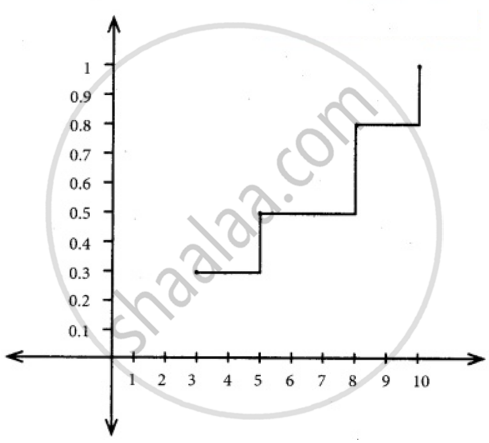
APPEARS IN
संबंधित प्रश्न
An urn contains 5 mangoes and 4 apples. Three fruits are taken at random. If the number of apples taken is a random variable, then find the values of the random variable and number of points in its inverse images
Choose the correct alternative:
Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed n times. Then the possible values of X are
Suppose that the time in minutes that a person has to wait at a certain station for a train is found to be a random phenomenon with a probability function specified by the distribution function
F(x) = `{{:(0",", "for" x ≤ 0),(x/2",", "for" 0 ≤ x < 1),(1/2",", "for" ≤ x < 2),(x/4",", "for" 2 ≤ x < 4),(1",", "for" x ≥ 4):}`
What is the probability that a person will have to wait (i) more than 3 minutes, (ii) less than 3 minutes and (iii) between 1 and 3 minutes?
Define dicrete random Variable
Distinguish between discrete and continuous random variables.
Explain the terms probability density function
What are the properties of discrete random variable
Choose the correct alternative:
The height of persons in a country is a random variable of the type
The probability function of a random variable X is given by
p(x) = `{{:(1/4",", "for" x = - 2),(1/4",", "for" x = 0),(1/2",", "for" x = 10),(0",", "elsewhere"):}`
Evaluate the following probabilities
P(0 ≤ X ≤ 10)
The probability density function of a continuous random variable X is
f(x) = `{{:("a" + "b"x^2",", 0 ≤ x ≤ 1),(0",", "otherwise"):}`
where a and b are some constants. Find Var(X)
