Advertisements
Advertisements
प्रश्न
लम्बवत् अक्षों के प्रमेय की उपपत्ति करें। [संकेत:(x, y) तल के लम्बवत् मूल बिन्दु से गुजरती अक्ष से किसी बिन्दु x – y की दूरी का वर्ग (x2 + y2) है।
उत्तर
लम्बवत् अक्षों की प्रमेय –
इस प्रमेय के अनुसार, “किसी समपटल का उसके तल के लम्बवत् तथा द्रव्यमान केन्द्र से जाने वाली अक्ष के परितः जड़त्व-आघूर्ण (Is), समपटल के तल में स्थित तथा द्रव्यमान केन्द्र से जाने वाली दो परस्पर लम्बवत् अक्षों के परितः समपटल के जड़त्व-आघूर्णी (Ix तथा Iy) के योग के बराबर होता है।”
अर्थात `"I"_"z" = "I"_"x" + "I"_"y"`
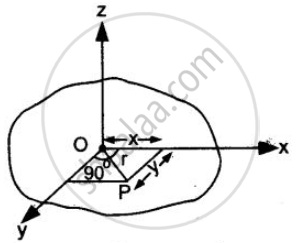
उपपत्ति - चित्र में x - y समतल में स्थित एक समपटल किया गया है तथा x तथा y - अक्ष समपटल के द्रव्यमान केंद्र से होकर गुजरती है। माना समपटल के किसी कण P का द्रव्यमान m है जिसके निर्देशांक (x , y) है अर्थात कण की x -अक्ष से दूरी y तथा y - अक्ष से दुरी x है। अतः x तथा y -अक्षों के परितः पटल के जड़त्व आघूर्ण क्रमशः
`"I"_"x" = ∑"my"^2` तथा `"I"_"y" = ∑"mx"^2` होंगे।
अब z-अक्ष पिण्ड के द्रव्यमान केंद्र से गुजरती है तथा x तथा y अक्षों के लम्बवत है; अतः समपटल के तल के भी लम्बवत है।
माना कण की z-अक्ष से दूरी r है, तब चित्र से,
`"r"^2 = "x"^2 + "y"^2` ...(1)
अतः z-अक्ष के परितः का जड़त्व -आघूर्ण
`"I"_"z" = ∑"mr"^2 = ∑ "m" ("x"^2 + "y"^2)` ...[समीकरण (1) से]
= ` ∑"mx"^2 + ∑"my"^2 = "I"_"y" + "I" _"x"`
अर्थात `"I"_"z" = "I"_"x" + "I"_"y"`
