Advertisements
Advertisements
प्रश्न
निम्न में से कौन n भुजाओं वाले एक समबहुभुज के बहिष्कोण के लिए सत्य नहीं है?
पर्याय
प्रत्येक बहिष्कोण = `360^circ/n`
बहिष्कोण = 180° – अंतःकोण
`n = 360^circ/"बहिष्कोण"`
प्रत्येक बहिष्कोण = `((n - 2) xx 180^circ)/n`
उत्तर
`bb("प्रत्येक बहिष्कोण" = ((n - 2) xx 180^circ)/n`
स्पष्टीकरण -
हम जानते हैं कि, (a) और (b) प्रत्येक बाह्य कोण का माप ज्ञात करने के सूत्र हैं, जब क्रमशः भुजाओं की संख्या और आंतरिक कोण का माप दिया गया हो और (c) बहुभुज की भुजाओं की संख्या ज्ञात करने का सूत्र है, जब बाह्य कोण दिया गया हो
अतः, विकल्प (d) में दिया गया सूत्र n भुजाओं वाले नियमित बहुभुज के बाह्य कोण के लिए सत्य नहीं है।
APPEARS IN
संबंधित प्रश्न
किसी त्रिभुज के एक ही क्रम के बहिष्कोणों का योग होता है –
उस समबहुभुज की भुजाओं की संख्या, जिसका प्रत्येक बहिष्कोण 45∘ माप का है, होगी –
किसी बहुभुज के एक ही क्रम में लिये गये सभी बहिष्कोणों का योग ______ होता है।
एक बहिष्कोण 72∘ वाले एक सम बहुभुज की भुजाओं की संख्या ______ है।
त्रिभुज एक ऐसा बहुभुज है जिसके एक ही क्रम में लिये गये बहिष्कोणों का योग उसके अंतःकोणों के योग का दोगुना होता है।
अंतःकोणों के योग और एक ही क्रम में लिये गये बहिष्कोणों के योग केवल चतुर्भुजों के लिए बराबर होते हैं।
यदि एक त्रिभुज के अंतःकोणों का अनुपात 1 : 2 : 3 हो, तो उसके बहिष्कोणों का अनुपात 3 : 2 : 1 होगा।
एक समबहुभुज के बहिष्कोण और अंतःकोण 1:5 के अनुपात में हैं। इस बहुभुज की भुजाओं की संख्या ज्ञात कीजिए।
नीचे दी गयी आकृति में, x का मान ज्ञात कीजिए।
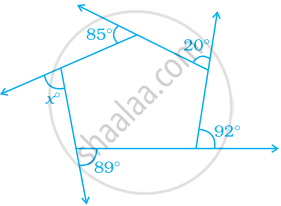
उन न्यूनकोणों की अधिकतम संख्या ज्ञात कीजिए जो एक उत्तल चतुर्भुज, उत्तल पंचभुज और उत्तल षड्भुज में हो सकते हैं। इस पैटर्न को देखिए और इस परिणाम को एक बहुभुज के लिए व्यापीकृत कीजिए।
