Advertisements
Advertisements
प्रश्न
निम्नलिखित कथनों को अभिगृहीत माना गया है :
- यदि दो रेखाएँ परस्पर प्रतिच्छेद करें तो शीर्षाभिमुख कोण बराबर नहीं होते हैं।
- यदि एक किरण एक रेखा पर खड़ी हो तो इस प्रकार प्राप्त दोनों आसन्न कोणों का योग 180° होता है।
क्या अभिगृहीतों का यह निकाय संगत है?
उत्तर
हम जानते हैं कि, यदि दो रेखाएँ परस्पर प्रतिच्छेद करती हैं, तो शीर्षाभिमुख कोण बराबर होते हैं। यह एक प्रमेय है, इसलिए दिया गया कथन I असत्य है और अभिगृहीत नहीं है।
साथ ही, हम यह भी जानते हैं कि यदि एक किरण एक रेखा पर खड़ी हो, तो इस प्रकार बने दो आसन्न कोणों का योग 180° के बराबर होता है। यह एक स्वयंसिद्ध है। इसलिए, दिया गया कथन II सत्य और एक अभिगृहीत है।
इस प्रकार, दिए गए कथनों में पहला असत्य है और दूसरा अभिगृहीत है।
अतः, स्वयंसिद्धों की दी गई प्रणाली सुसंगत नहीं है।
APPEARS IN
संबंधित प्रश्न
निम्नलिखित कथन सत्य हैं या असत्य हैं? अपने उत्तर के लिए कारण दीजिए।
आकृति में, यदि AB = PQ और PQ = XY, तो AB = XY होगा।

निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
समांतर रेखाएँ
निम्नलिखित पद की परिभाषा दीजिए। क्या इनके लिए कुछ ऐसे पद हैं, जिन्हें परिभाषित करने की आवश्यकता है? वे क्या हैं और आप इन्हें कैसे परिभाषित कर पाएँगे?
रेखाखंड
यूक्लिड की पाँचवीं अभिधारणा को अन्य अभिधारणाओं और अभिगृहीतों का प्रयोग करते हुए, सिद्ध करने के प्रयासों के फलस्वरूप अन्य अनेक ज्यामितियों की खोज हुई।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
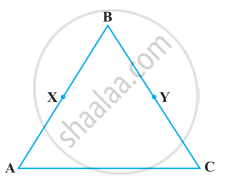
निम्नलिखित आकृति में, हमें प्राप्त है :
BX = `1/2` AB, BY = `1/2` BC तथा AB = BC है। दर्शाइए कि BX = BY है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
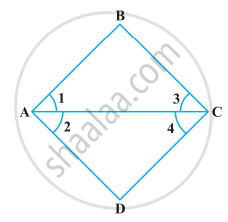
निम्नलिखित आकृति में, ∠1 = ∠3 और ∠2 = ∠4 है। दर्शाइए कि ∠A = ∠C है।
निम्नलिखित प्रश्न को उपयुक्त यूक्लिड की अभिगृहीत का प्रयोग करते हुए, हल कीजिए :
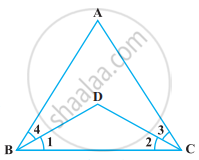
निम्नलिखित आकृति में, ∠ABC = ∠ACB और ∠3 = ∠4 है। दर्शाइए कि ∠1 = ∠2 है।
निम्नलिखित आकृति में AB = BC, M रेखाखंड AB का मध्य-बिंदु है और N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AM = NC है।
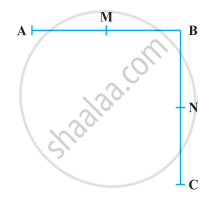
निम्नलिखित आकृति में BM = BN हैं, M रेखाखंड AB का मध्य-बिंदु है तथा N रेखाखंड BC का मध्य-बिंदु है। दर्शाइए कि AB = BC है।

निम्नलिखित कथन को पढ़िए :
एक समबाहु त्रिभुज तीन रेखाखंडों से बना एक बहुभुज है जिनमें से दो रेखाखंड तीसरे रेखाखंड के बराबर हैं तथा इसका प्रत्येक कोण 60° का है।
इस परिभाषा में, उन पदों को परिभाषित कीजिए जिन्हें आप आवश्यक समझते हैं। क्या इसमें कोई अपरिभाषित पद है? क्या आप इसका औचित्य दे सकते हैं कि एक समबाहु त्रिभुज के सभी कोण और सभी भुजाएँ बराबर होती हैं।
