Advertisements
Advertisements
प्रश्न
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`1/(2x) - 1/y = -1, 1/x + 1/(2y) = 8, x, y ≠ 0`
उत्तर
दिए गए रैखिक समीकरणों के युग्म हैं।
`1/(2x) - 1/y` = – 1 ......(i)
और `1/x + 1/(2y)` = 8, x, y ≠ 0 ......(ii)
u = `1/x` और v = `1/y`,
तब उपरोक्त समीकरण बन जाते हैं।
`u/2 - v` = – 1
⇒ u – 2v = – 2 ....(iii)
और `u + v/2 = 8`
⇒ 2u + v = 16 .....(iv)
समीकरण (iv) को 2 से गुणा करने और फिर समीकरण (iii) के साथ जोड़ने पर, हमें प्राप्त होता है।
4u + 2v = 32
u – 2v = –2
5u = 30
5u = 30
⇒ u = 6
अब, समीकरण (iv) में u का मान रखें, हमें मिलता है।
2 × 6 + ν = 16
⇒ v = 16 – 12 = 4
⇒ v = 4
∴ x = `1/u = 1/6`
और y = `1/v = 1/4`
अतः, x और y के आवश्यक मान क्रमशः 1/6 और 1/4 हैं।
APPEARS IN
संबंधित प्रश्न
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे व्रज-गुणन विधि से ज्ञात कीजिए।
2x + y = 5
3x + 2y = 8
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे व्रज-गुणन विधि से ज्ञात कीजिए।
3x - 5y = 20
6x - 10y = 40
निम्न रैखिक समीकरणों के युग्मों में से किसका एक अद्वितीय हल है, किसका कोई हल नहीं है या किसके अपरिमित रूप से अनेक हल हैं। अद्वितीय हल की स्थिति में, उसे व्रज-गुणन विधि से ज्ञात कीजिए।
x - 3y - 7 = 0
3x - 3y - 15 = 0
निम्नलिखित आयत में x और y के मान ज्ञात कीजिए:
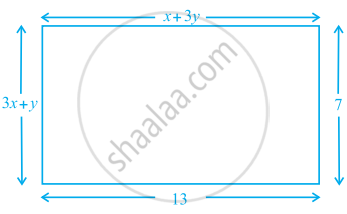
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`x/3 + y/4 = 4, (5x)/6 - y/4 = 4`
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`4x + 6/y = 15, 6x - 8/y = 14, y ≠ 0`
निम्नलिखित समीकरण-युग्म को हल कीजिए:
43x + 67y = – 24, 67x + 43y = 24
निम्नलिखित समीकरण-युग्म को हल कीजिए:
`(2xy)/(x + y) = 3/2, (xy)/(2x - y) = (-3)/10, x + y ≠ 0, 2x - y ≠ 0`
समीकरण `x/10 + y/5 - 1` = 0 और `x/8 + y/6` = 15 के युग्म का हल ज्ञात कीजिए। इसके बाद λ ज्ञात कीजिए, यदि y = λx + 5 है।
एक मोटरबोट धारा के प्रतिकूल 30 km और धारा के अनुकूल 28 km जाने में 7 घंटे का समय लगाती है। वह धारा के प्रतिकूल 21 km जाकर 5 घंटे में वापस आ सकती है। शांत जल में नाव की चाल और धारा की चाल ज्ञात कीजिए।
