Advertisements
Advertisements
प्रश्न
निर्धारित कीजिए कि क्या बिंदु (1, 5), (2, 3) और (-2, -11) संरेखी हैं।
उत्तर १
मान लीजिए कि बिंदु (1, 5), (2, 3) और (−2, −11) क्रमशः दिए गए त्रिभुज के शीर्ष A, B और C को दर्शाते हैं। माना A = (1, 5), B = (2, 3), C = (-2, -11)
Let A = (1, 5), B = (2, 3), C = (-2, -11)
∴ AB = `sqrt((1-2)^2+(5-3)^2)`
BC = `sqrt((2-(-2))^2 + (3-(-11))^2)`
= `sqrt(4^2+14^2)`
= `sqrt(16+196)`
= `sqrt(212)`
= `2sqrt53`
CA = `sqrt((1-(-2))^2 + (5-(-11))^2)`
= `sqrt(3^2+16^2)`
= `sqrt(9+256)`
= `sqrt(265)`
Since AB + BC ≠ CA
इसलिए, बिंदु (1, 5), (2, 3) और (−2, −11) संरेख नहीं हैं।
उत्तर २
मान लीजिए दिए हुए बिन्दु P(1, 5), Q(2, 3) और R(-2, -11) हैं।
अब PQ = `sqrt((2 - 1)^2 + (3 - 5)^2)`
= `sqrt((1)^2 + (-2)^2)`
= `sqrt(1 + 4)`
= `sqrt5`
QR = `sqrt((-2 - 2)^2 + (-11 - 3)^2)`
= `sqrt((-4)^2 + (-14)^2)`
= `sqrt(16 + 196)`
=` sqrt212`
एवं RP = `sqrt((1 + 2)^2 + (5 + 11)^2)`
= `sqrt((3)^2 + (16)^2)`
= `sqrt(9 + 256)`
= `sqrt265`
लेकिन
`sqrt5 + sqrt212 ≠ sqrt265`
अतः दिए हुए बिन्दु सरेख नहीं हैं।
APPEARS IN
संबंधित प्रश्न
यदि बिंदु L(x, 7) और M(1, 15) के बीच की दूरी 10 हो, तो x का मान ज्ञात कीजिए।
निम्नलिखित बिंदुओं को जोड़नेवाले रेखाखंड त्रिभुज बना सकते हैं क्या? यदि त्रिभुज बनता हो तो भुजाओं के आधार पर त्रिभुज का प्रकार लिखिए।
L(6, 4), M(-5, -3), N(-6, 8)
सिद्ध कीजिए, कि A(4, -1), B(6, 0), C(7, -2) और D(5, -3) वर्ग के शीर्ष बिंदु हैं।
y का वह मान ज्ञात कीजिए, जिसके लिए बिंदु P(2, -3) और Q(10, y) के बीच की दूरी 10 मात्रक है।
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(-3, 5), (3, 1), (0, 3), (-1, -4)
किसी वर्ग के दो सम्मुख शीर्ष (-1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।
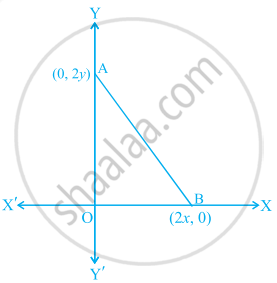
आकृति में दर्शाए गए त्रिभुज AOB के तीनों शीर्षो से समदूरस्थ बिंदु के निर्देशांक ______ हैं।
बिंदु A(4, 3), B(6, 4), C(5, –6) और D(–3, 5) एक समांतर चतुर्भुज के शीर्ष हैं।
एक वृत्त का केंद्र मूलबिंदु पर है तथा एक बिंदु P(5, 0) इस वृत्त पर स्थित है। बिंदु Q(6, 8) इस वृत्त के बाहर स्थित है।
बिंदुओं A(–5, 6), B(–4, –2) और C(7, 5) से बनने वाले त्रिभुज का प्रकार बताइए।
