Advertisements
Advertisements
प्रश्न
Find the minimum colatitude which can directly receive a signal from a geostationary satellite.
उत्तर
Consider that B is the position of the geostationary satellite.
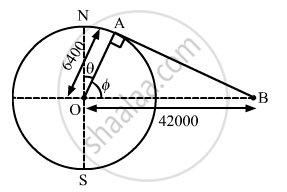
In the given figure,
\[\phi\] is the latitude and θ is the colatitude of a place which can directly receive a signal from a geostationary satellite.
In triangle OAB, we have:
\[\cos \phi = \frac{6400}{42000}\]
\[ = \frac{16}{106} = \frac{8}{53}\]
\[i . e . , \phi = \cos^{- 1} \frac{8}{53}\]
\[ = \cos^{- 1} 0 . 15\]
\[\text { Now }, \theta = \frac{\pi}{2} - \phi\]
\[ \Rightarrow \theta = \frac{\pi}{2} - \cos^{- 1} 0 . 15\]
\[ \Rightarrow \theta = \sin^{- 1} 0 . 15\]
APPEARS IN
संबंधित प्रश्न
No part of India is situated on the equator. Is it possible to have a geostationary satellite which always remains over New Delhi?
Two satellites A and B move round the earth in the same orbit. The mass of B is twice the mass of A.
A body stretches a spring by a particular length at the earth's surface at the equator. At what height above the south pole will it stretch the same spring by the same length? Assume the earth to be spherical.
A pendulum having a bob of mass m is hanging in a ship sailing along the equator from east to west. When the ship is stationary with respect to water the tension in the string is T0. (a) Find the speed of the ship due to rotation of the earth about its axis. (b) Find the difference between T0 and the earth's attraction on the bob. (c) If the ship sails at speed v, what is the tension in the string? Angular speed of earth's rotation is ω and radius of the earth is R.
(a) Find the radius of the circular orbit of a satellite moving with an angular speed equal to the angular speed of earth's rotation. (b) If the satellite is directly above the North Pole at some instant, find the time it takes to come over the equatorial plane. Mass of the earth = 6 × 1024 kg.
Answer the following question.
Define the binding energy of a satellite.
Answer the following question.
What is periodic time of a geostationary satellite?
Draw a labelled diagram to show different trajectories of a satellite depending upon the tangential projection speed.
Answer the following question in detail.
Why an astronaut in an orbiting satellite has a feeling of weightlessness?
Answer the following question in detail.
Obtain an expression for the critical velocity of an orbiting satellite. On what factors does it depend?
Calculate the kinetic energy, potential energy, total energy and binding energy of an artificial satellite of mass 2000 kg orbiting at a height of 3600 km above the surface of the Earth.
Given: G = 6.67 × 10-11 Nm2/kg2
R = 6400 km, M = 6 × 1024 kg
Solve the following problem.
Calculate the value of the universal gravitational constant from the given data. Mass of the Earth = 6 × 1024 kg, Radius of the Earth = 6400 km, and the acceleration due to gravity on the surface = 9.8 m/s2.
Solve the following problem.
What is the gravitational potential due to the Earth at a point which is at a height of 2RE above the surface of the Earth?
(Mass of the Earth is 6 × 1024 kg, radius of the Earth = 6400 km and G = 6.67 × 10–11 N m2 kg–2)
Which of the following statements is CORRECT in respect of a geostationary satellite?
There is no atmosphere on moon because ____________.
Assuming that the earth is revolving around the sun in circular orbit of radius 'R', the angular momentum is directly proportional to rn. The value of 'n' is ______.
If the Earth-Sun distance is held constant and the mass of the Sun is doubled, then the period of revolution of the earth around the Sun will change to ____________.
The ratio of energy required to raise a satellite to a height `(2R)/3` above earth's surface to that required to put it into the orbit at the same height is ______.
R = radius of the earth
