Advertisements
Advertisements
प्रश्न
The separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
(a) Charge on the capacitor
(b) Potential difference across the capacitor
(c) Energy of the capacitor
(d) Energy density between the plates
उत्तर
(b) Potential difference across the capacitor
(c) Energy of the capacitor.
Because the charge always remains conserved in an isolated system, it will remain the same.
Now ,
`V = (Qd)/(∈_0A)`
Here, Q, A and d are the charge, area and distance between the plates, respectively.
Thus, as d increases, V increases.
Energy is given by `E = (qV)/2`
So , it will also increase .
Energy density u , that is , energy stored per unit volume in the electric field is given by `u = 1/2∈_0E^2`
So , u will remain constant with increase in distance between the plates .
APPEARS IN
संबंधित प्रश्न
Two capacitors of unknown capacitances C1 and C2 are connected first in series and then in parallel across a battery of 100 V. If the energy stored in the two combinations is 0.045 J and 0.25 J respectively, determine the value of C1 and C2. Also calculate the charge on each capacitor in parallel combination.
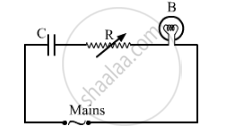
A capacitor 'C', a variable resistor 'R' and a bulb 'B' are connected in series to the ac mains in circuit as shown. The bulb glows with some brightness. How will the glow of the bulb change if (i) a dielectric slab is introduced between the plates of the capacitor, keeping resistance R to be the same; (ii) the resistance R is increased keeping the same capacitance?
Deduce an expression for equivalent capacitance C when three capacitors C1, C2 and C3 connected in parallel.
The plates of a parallel-plate capacitor are given equal positive charges. What will be the potential difference between the plates? What will be the charges on the facing surfaces and on the outer surfaces?
If the capacitors in the previous question are joined in parallel, the capacitance and the breakdown voltage of the combination will be
A parallel-plate capacitor has plates of unequal area. The larger plate is connected to the positive terminal of the battery and the smaller plate to its negative terminal. Let Q, and Q be the charges appearing on the positive and negative plates respectively.
Each plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a batter. Now,
(a) the facing surfaces of the capacitor have equal and opposite charges
(b) the two plates of the capacitor have equal and opposite charges
(c) the battery supplies equal and opposite charges to the two plates
(d) the outer surfaces of the plates have equal charges
The plates of a capacitor are 2⋅00 cm apart. An electron-proton pair is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as the electron reaches the positive plate. At what distance from the negative plate was the pair released?
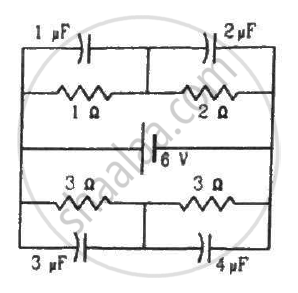
Find the charges on the four capacitors of capacitances 1 μF, 2 μF, 3 μF and 4 μF shown in the figure.
A parallel-plate capacitor having plate area 20 cm2 and separation between the plates 1⋅00 mm is connected to a battery of 12⋅0 V. The plates are pulled apart to increase the separation to 2⋅0 mm. (a) Calculate the charge flown through the circuit during the process. (b) How much energy is absorbed by the battery during the process? (c) Calculate the stored energy in the electric field before and after the process. (d) Using the expression for the force between the plates, find the work done by the person pulling the plates apart. (e) Show and justify that no heat is produced during this transfer of charge as the separation is increased.
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
Three capacitors of capacitance `C_1 = 3muf` , `C_2 = 6muf` , `C_3 = 10muf` , are connected to a 10V battery as shown in figure 3 below :
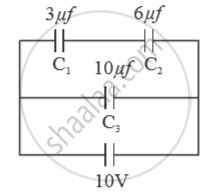
Calculate :
(a) Equivalent capacitance.
(b) Electrostatic potential energy stored in the system
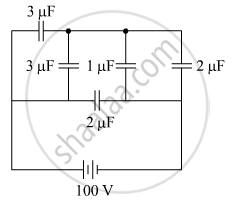
The figure shows a network of five capacitors connected to a 100 V supply. Calculate the total energy stored in the network.
Two parallel plate capacitors X and Y, have the same area of plates and same separation between plates. X has air and Y with dielectric of constant 2, between its plates. They are connected in series to a battery of 12 V. The ratio of electrostatic energy stored in X and Y is ______.
Capacitors connected in series have ______
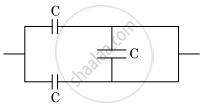
The equivalent capacitance of the combination shown in the figure is ______.
The total charge on the system of capacitors C1 = 1 µF, C2 = 2 µF, C3 = 4 µF and C4 = 3 µF connected in parallel is ______. (Assume a battery of 20 V is connected to the combination)
The capacitors, each of 4 µF are to be connected in such a way that the effective capacitance of the combination is 6 µF. This can be achieved by connecting ______.
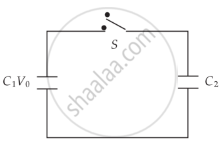
A capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with an uncharged capacitor of capacity C2 as shown in the adjoining figure. Find the ratio of energies before and after the connection of switch S.