Advertisements
Advertisements
प्रश्न
ΔPBC and ΔQBC are two isosceles triangles on the same base. Show that the line PQ is bisector of BC and is perpendicular to BC.
उत्तर
Given: ΔPBC and ΔQBC are two isosceles triangles on the same base BC.
To prove: Line PQ is the perpendicular bisector of BC.
Proof: In ΔPBC, PB = PC
Since, the locus of a point equidistant from B and C is the perpendicular bisector of 1 of the line segment BC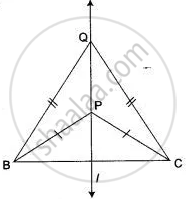
∴ P lies on 1
Similarly Q lies on 1
Therefore, PQ is the perpendicular bisector of BC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Describe the locus of points at a distance 2 cm from a fixed line.
Describe the locus of the centre of a wheel of a bicycle going straight along a level road.
Describe the locus of a stone dropped from the top of a tower.
Describe the locus of the door handle, as the door opens.
Describe the locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
Describe the locus of the centres of all circles passing through two fixed points.
Describe the locus of points at distances less than 3 cm from a given point.
Sketch and describe the locus of the vertices of all triangles with a given base and a given altitude.
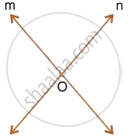
In the given figure, obtain all the points equidistant from lines m and n; and 2.5 cm from O.
Find the locus of the centre of a circle of radius r touching externally a circle of radius R.
