Advertisements
Advertisements
प्रश्न
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?
उत्तर
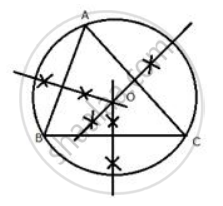
Yes, the perpendicular bisector of BC will pass through O.
APPEARS IN
संबंधित प्रश्न
Using a ruler and a compass, construct a triangle ABC in which AB = 7 cm, ∠CAB = 60° and AC = 5 cm. Construct the locus of :
- points equidistant from AB and AC.
- points equidistant from BA and BC.
Hence construct a circle touching the three sides of the triangle internally.
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Using a ruler and compasses only:
1) Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ABC = 120°
2) In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
3) Measure ∠BCP.
Using ruler and compasses only,
- Construct a triangle ABC with the following data :
Base AB = 6 cm, BC = 6.2 cm and ∠CAB = 60°. - In the same diagram, draw a circle which passes through the points A, B and C and mark its center O.
- Draw a perpendicular from O to AB which meets AB in D.
- Prove that : AD = BD.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
- What do you call the point O?
- What is the relation between the distances OA, OB and OC?
- Does the perpendicular bisector of BC pass through O?
Contruct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incricle.
Draw a line segment OA , 5 cm long. AT O , using ruler and compasses only, construct OB such that , ∠ AOB = 37.5° construct a circle to touch OA at A and to touch OB at B.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC?
Using ruler and compass only, construct a triangle ABC such that AB = 5 cm, ABC = 75°, and the radius of the circumcircle of triangle ABC is 3.5 cm. On the same diagram, construct a circle, touching AB at its middle point and also touching the side AC.
Construct a ΔABC with base BC = 3.5 cm, vertical angle ∠ BAC = 45°, and median through the vertex A is 3.5 cm. Write also the steps of construction.
