Advertisements
Advertisements
प्रश्न
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
Does the perpendicular bisector of BC pass through O?
उत्तर
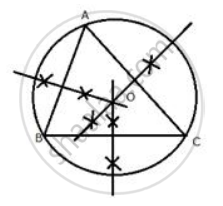
Yes, the perpendicular bisector of BC will pass through O.
APPEARS IN
संबंधित प्रश्न
Construct a regular hexagon of side 5 cm. Hence construct all its lines of symmetry and name them.
Using ruler and compass only, construct a ΔABC such that BC = 5 cm and AB = 6.5
cm and ∠ABC = 120°
1) Construct a circum-circle of ΔABC
2) Construct a cyclic quadrilateral ABCD, such that D is equidistant from AB and BC.
Construct a ΔABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Using ruler and compasses only,
- Construct triangle ABC, having given BC = 7 cm, AB – AC = 1 cm and ∠ABC = 45°.
- Inscribe a circle in the ΔABC constructed in (i) above. Measure its radius.
Using a ruler and compasses only:
- Construct a triangle ABC with the following data: AB = 3.5 cm, BC = 6 cm and ∠ABC = 120°.
- In the same diagram, draw a circle with BC as diameter. Find a point P on the circumference of the circle which is equidistant from AB and BC.
- Measure ∠BCP.
Construct Δ ABC in which AB = 5 cm, BC = 4. 5 cm and ∠ ABC = 60" .. Construct a cirde to circumscribe. Δ ABC.
Using ruler and compasses only, construct Δ ABC in which BC=7.5 cm, ∠ ABC = 60° and AC - AB= 1.5 cm. Inscribe a circle in the Δ ABC and measure its radius.
Construct a triangle ABC in which AB = 5 cm, BC = 6.8 cm and median AD = 4.4 cm. Draw incircle of this triangle.
Construct a Δ ABC with BC = 6.5 cm, AB = 5.5 cm, AC = 5 cm. Construct the incircle of the triangle. Measure and record the radius of the incircle.
Ruler and compasses only may be used in this question. All constructions lines and arcs must be clearly shown, and the be sufficient length and clarity to permit assessment:
(i) Construct a triangle ABC, in which AB = 9 cm, BC = 10 cm and angle ABC = 45°.
(ii) Draw a circle, with center A and radius 2.5 cm. Let it meet AB at D.
(iii) Construct a circle to touch the circle with center A externally at D and also to touch the line BC.
