Advertisements
Advertisements
प्रश्न
Point P(– 4, 2) lies on the line segment joining the points A(– 4, 6) and B(– 4, – 6).
पर्याय
True
False
उत्तर
This statement is True.
Explanation:
Plotting the points P(– 4, 2), A(– 4, 6) and B(– 4, – 6) on a graph paper and connecting the points we get the graph,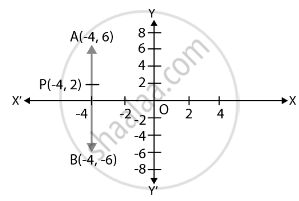
Hence, from the graph it is clear that, point P(– 4, 2) lies on the line segment joining the points A(– 4, 6) and B(– 4, – 6).
APPEARS IN
संबंधित प्रश्न
If (−2, 3), (4, −3) and (4, 5) are the mid-points of the sides of a triangle, find the coordinates of its centroid.
In Fig. 14.36, a right triangle BOA is given C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.

We have a right angled triangle,`triangle BOA` right angled at O. Co-ordinates are B (0,2b); A (2a, 0) and C (0, 0).
In what ratio is the line segment joining the points (-2,-3) and (3, 7) divided by the y-axis? Also, find the coordinates of the point of division.
Show that the following points are the vertices of a rectangle.
A (2, -2), B(14,10), C(11,13) and D(-1,1)
Find the ratio in which the pint (-3, k) divide the join of A(-5, -4) and B(-2, 3),Also, find the value of k.
If the points P (a,-11) , Q (5,b) ,R (2,15) and S (1,1). are the vertices of a parallelogram PQRS, find the values of a and b.
Find the area of quadrilateral ABCD whose vertices are A(-5, 7), B(-4, -5) C(-1,-6) and D(4,5)
Find the centroid of ΔABC whose vertices are A(2,2) , B (-4,-4) and C (5,-8).
Find the ratio in which the point (−3, k) divides the line-segment joining the points (−5, −4) and (−2, 3). Also find the value of k ?
Find the ratio in which the line segment joining the points A(3, 8) and B(–9, 3) is divided by the Y– axis.
Point P(x, 4) lies on the line segment joining the points A(−5, 8) and B(4, −10). Find the ratio in which point P divides the line segment AB. Also find the value of x.
The abscissa of any point on y-axis is
If the points A(−1, −4), B(b, c) and C(5, −1) are collinear and 2b + c = 4, find the values of b and c.
Write the perimeter of the triangle formed by the points O (0, 0), A (a, 0) and B (0, b).
Write the formula for the area of the triangle having its vertices at (x1, y1), (x2, y2) and (x3, y3).
If A(4, 9), B(2, 3) and C(6, 5) are the vertices of ∆ABC, then the length of median through C is
If A(x, 2), B(−3, −4) and C(7, −5) are collinear, then the value of x is
Write the X-coordinate and Y-coordinate of point P(– 5, 4)
Point (0, –7) lies ______.
Abscissa of all the points on the x-axis is ______.
